VERIFYING BASIC PROPORTIONALITY THEOREM EXAMPLES

Example 1 :

In the figure given below, if LM ∥ CB and LN ∥ CD prove that AM/AB = AN/AD.

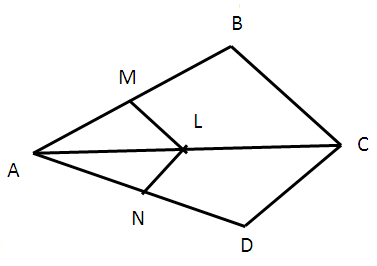
Solution :

In triangle ABC

LM is parallel to BC

AM/MB  =  AL/LC ------- (1)

NL is parallel to DC

AN/ND  =  AL/LC  ------(2)

(1) = (2)

AM/MB  =  AN/ND

Hence proved.

Example 2 :

In the figure given below, DE ∥ AC and DF ∥ AE. prove that BF/FE  =  BE/EC.

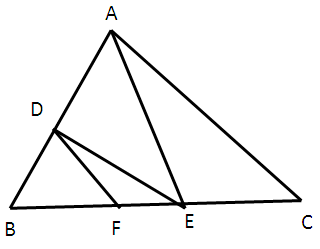
Solution :

In triangle ABC, 

The side DE and AC are parallel. So, we have 

BD/DA  =  BE/EC -----(1)

In triangle AEB,

The side DF and AE are parallel. So, we have 

BD/DA = BF/FE -----(2)

(1)  =  (2)

BE/EC  =  BF/FE

Hence proved.

Example 3 :

In the figure given below, DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR.

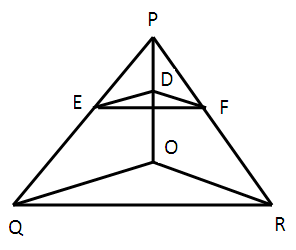
Solution :

In triangle PQO,

The sides DE and OQ are parallel. So, we have

PE/EQ  =  PD/DO----(1)

In triangle POR,

The sides DE and OQ are parallel. So, we have 

PF/FR  =  PD/DO  ------(2)

(1)  =  (2)

PE/EQ  =  PF/FR

By converse of BPT theorem, EF is parallel to QR.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.