USING PROPORTIONAL RELATIONSHIPS TO FIND DISTANCE ON A MAP
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A scale drawing is a drawing of a real object that is proportionally smaller or larger than the real object.
A scale is a ratio between two sets of measurements. It shows how a dimension in a scale drawing is related to the actual object.
A map is a scale drawing. The measurements on a map are in proportion to the actual distances.
If 1 inch on a map equals an actual distance of 2 miles, the scale is 1 inch = 2 miles. We can write a scale as a rate to solve problems.
Example 1 :
The distance between two schools on Lehigh Avenue is shown on the map. If the scale is 1 inch = 2 miles, what is the actual distance between the schools?
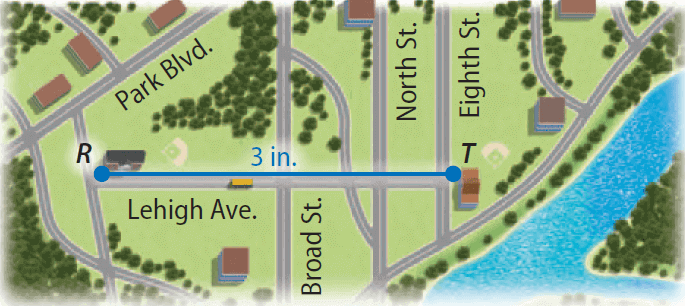
Solution :
Step 1 :
Write a proportion using the scale as a unit rate.
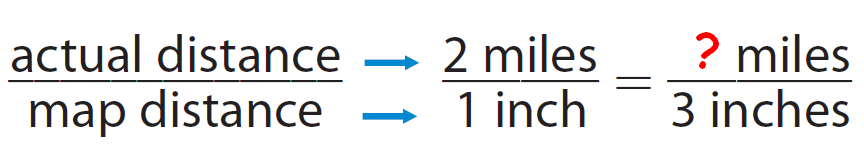
Step 2 :
Use the proportion to find the distance.
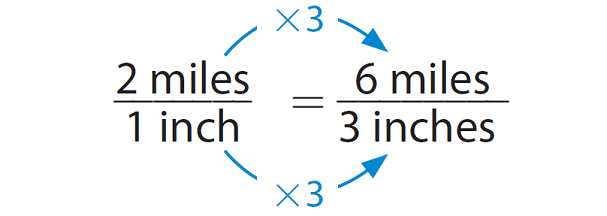
Because 1 × 3 = 3, multiply 2 by 3.
So, the actual distance between the two schools is 6 miles.
Example 2 :
The distance between Sandville and Lewiston is shown on the map. If the scale is 1 inch = 20 miles, what is the actual distance between the towns?
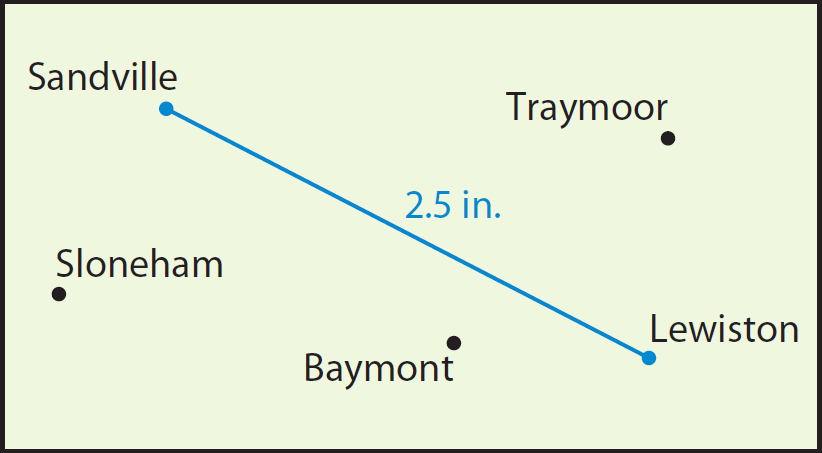
Solution :
Step 1 :
Write a proportion using the scale as a unit rate.
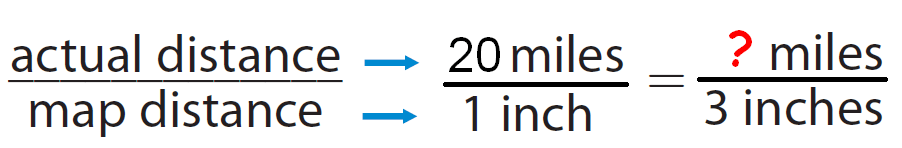
Step 2 :
Use the proportion to find the distance.
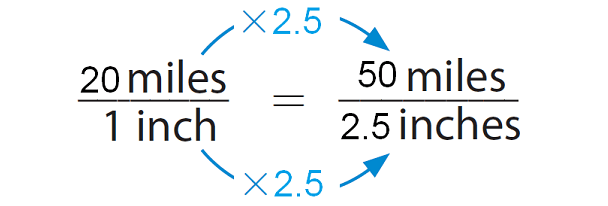
Because 1 × 2.5 = 2.5, multiply 20 by 2.5.
So, the actual distance between the towns is 50 miles.
Example 3 :
The actual distance between two towns is 90 miles. If the scale is 1 inch = 30 miles, what is the distance between the two towns on the map?
Solution :
Step 1 :
Write a proportion using the scale as a unit rate.
Actual distance / map distance = 30/1 = 90/?.
Step 2 :
Use the proportion to find the distance.
30/1 = (30 x 3)/(1 x 3) = 90/3
Because 30 × 3 = 90, multiply 1 by 3.
So, the distance between the towns on the map is 3 inches.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

