USING MEAN ABSOLUTE  DEVIATION

The mean absolute deviation can be used to answer statistical questions in the real world. Many of these questions may have implications for the operation of various businesses.

Example 1 :

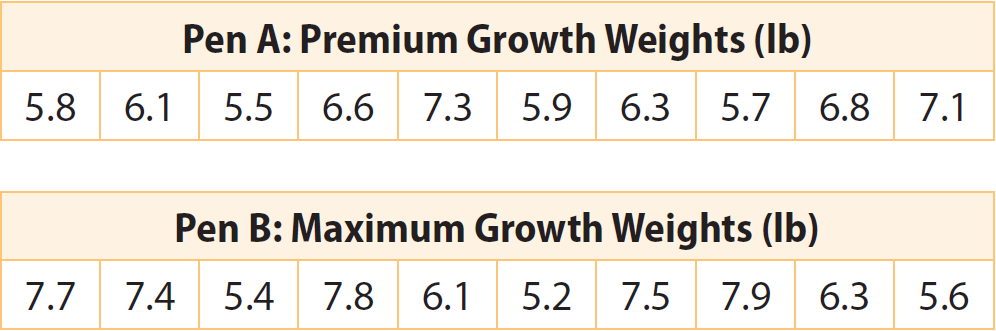
A chicken farmer wants her chickens to all have about the same weight. She is trying two types of feed to see which type produces the best results. All the chickens in Pen A are fed Premium Growth feed, and all the chickens in Pen B are fed Maximum Growth feed. The farmer records the weights of the chickens in each pen in the tables below. Which chicken feed produces less variability in weight ?

Solution :

Step 1 : 

Find the mean weight of the chickens in each pen. Round your answers to the nearest tenth.

Pen A  =  (5.8+6.1+5.5+6.6+7.3+5.9+6.3+5.7+6.8+7.1) / 10

Pen A  =  63.1 / 10

Pen A  =  6.31

Pen A   ≈  6.3

Pen B  =  (7.7+7.4+5.4+7.8+6.1+5.2+7.5+7.9+6.3+5.6) / 10

Pen A  =  66.9 / 10

Pen A  =  6.69

Pen A   ≈  6.7

Step 2 : 

Find the absolute deviations from the mean for each of the weights.

The absolute deviations from the mean for Pen A are the distance of each weight from 6.3 lb.

|5.8 - 6.3|  =  |-0.5|  =  0.5

|6.1 - 6.3|  =  |-0.2|  =  0.2

|5.5 - 6.3|  =  |-0.8|  =  0.8

|6.6 - 6.3|  =  |0.3|  =  0.3

|7.3 - 6.3|  =  |1.0|  =  1.0

|5.9 - 6.3|   =  |-0.4|  =  0.4

|6.3 - 6.3|  =  |0|  =  0

|5.7 - 6.3|  =  |-0.6|  =  0.6

|6.8 - 6.3|  =  |0.5|  =  0.5

|7.1 - 6.3|  =  |0.8|  =  0.8

The absolute deviations from the mean for Pen B are the distance of each weight from 6.7 lb.

|7.7 - 6.7|  =  |1.0|  =  1.0

|7.4 - 6.7|  =  |0.7|  =  0.7

|5.4 - 6.7|  =  |-1.3|  =  1.3

|7.8 - 6.7|  =  |1.1|  =  1.1

|6.1 - 6.7|  =  |-0.6|  =  0.6

|5.2 - 6.7|  =  |-1.5|  =  1.5

|7.5 - 6.7|  =  |0.8| =  0.8

|7.9 - 6.7|  =  |1.2|  =  1.2

|6.3 - 6.7|  =  |-0.4|  =  0.4

|5.6 - 6.7|  =  |-1.1|  =  1.1

Step 3 :

Calculate the mean absolute deviation for the chickens in each pen. Round your answers to the nearest tenth.

MAD for Pen A is

=  (0.5+0.2+0.8+0.3+1.0+0.4+0+0.6+0.5+0.8) / 10

MAD for Pen A  =  5.1 / 10

MAD for Pen A  =  0.51

MAD for Pen A  ≈ 0.5 lb

MAD for Pen B is

=  (1.0+0.7+1.3+1.1+0.6+1.5+0.8+1.2+0.4+1.1) / 10

MAD for Pen B  =  9.7 / 10

MAD for Pen B  =  0.97

MAD for Pen B  ≈ 1.0 lb

Since Pen A’s MAD is less, Premium Growth feed produces less variability in weight.

Example 2 : 

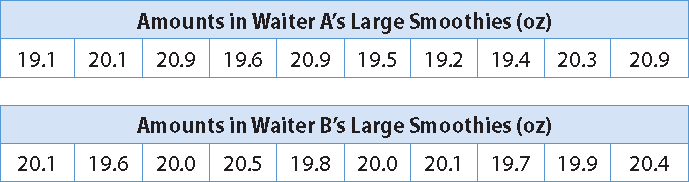
Two waiters at a cafe each served 10 large fruit smoothies. The amount in each large smoothie is shown below. Which waiter’s smoothies showed less variability ?

Solution :

The MAD for Waiter A is 0.6 oz, and the MAD for Waiter B is 0.2 oz, so Waiter B’s smoothies showed less variability.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.