USING LAWS OF SIN FINDING THE UNKNOWN SIDE

The sine law is a relationship between the sides and angles in any triangle. Let ABC be any triangle, where a, b, and c represent the measures of the sides opposite ∠A, ∠B, and ∠C, respectively. 

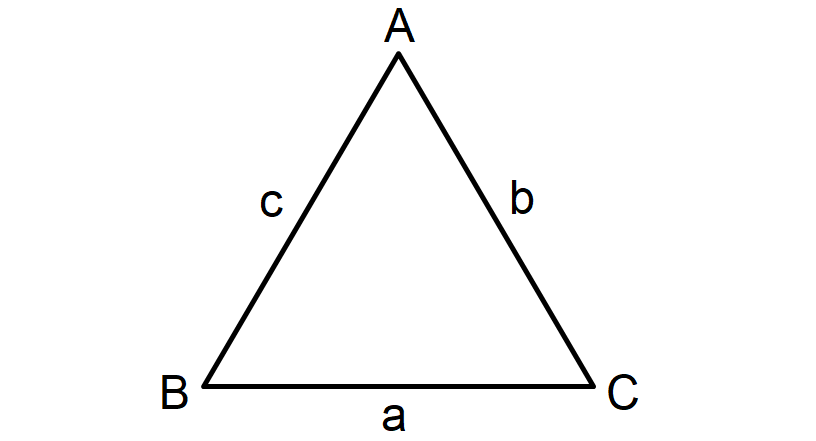
a/sin A  =  b/sin B  =  c/sin C

(or)

sin A/a  =  sin B/b  =  sin C/c

Question :

Using Laws of Sin Finding the Unknown Side. Round lengths to the nearest tenth of a unit and angle measures to the nearest degree.

1. Solve for the unknown side or angle in each.

a) a/sin 35°  =  10/sin 40°

Solution :

a/sin 35°  =  10/sin 40°

a/(0.5735)  =  10/(0.6427)

a /0.5735  =  15.56  

a  =  15.56 (0.5735)

a  =  8.93

Hence the unknown side measures approximately 8.9 units

(b)  b/sin 48°  =  65/sin 75°

Solution :

b/sin 48°  =  65/sin 75°

b/0.7431  =  65/0.9659

b/0.7431  =  67.29

b  =  67.29(0.7431)

b  =  50.00

Hence the unknown side measures 50.

(c)  sin θ/12  =  sin 50°/65

Solution :

sin θ/12  =  sin 50°/65

sin θ/12  =  0.7660/65

sin θ/12  =  0.012

sin θ  =  0.012(12)

sin θ  =  0.144

Hence the missing angle is 8°

(iv)  sin A/25  =  sin 62/32

Solution :

sin A/25  =  sin 62°/32

sin A/25  =  0.8829/32

sin A/25  =  0.0276

sin A  =  0.0276(25)

sin A  =  0.6897

A  =  43.6°

Hence the required angle is 43.6°

Question 2 :

Determine the length of AB in each.

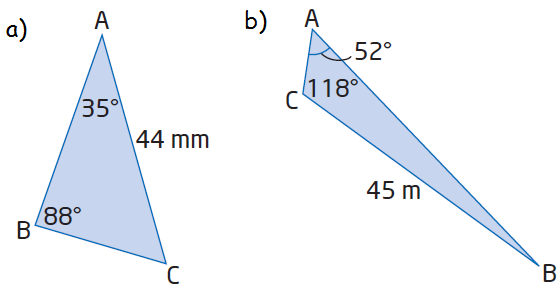
Solution :

(a)  In the triangle given above, the side which is opposite to angle A is known as "a", opposite to angle B and C are known as b and c respectively.

BC  = a, CA  =  b and AB  =  c.

We need to find the length of AB, that is A.

<A + <B  + <C  =  180

35 + 88 + <C  =  180

<C  =  180 - 123

<C  =  57

a/sin 35  =  b/sin 88 =  c/sin 57

a/sin 35  =  44/sin 88 =  AB/sin 57

44/0.9993  =  AB/0.8386

44.03  =  AB/0.8386

AB  =  44.03(0.8386)

AB  =  36.92 mm

Hence the length of side AB is 36.92 mm.

(b)  BC  = a  =  45, CA  =  b and AB  =  c.

We need to find the length of AB. That is c.

<A + <B  + <C  =  180

52 + <B + 118  =  180

<B  =  180 - 170

<B  =  10

a/sin 52  =  b/sin 10 =  c/sin 118

45/sin 52  =  b/sin 10 =  c/sin 118

45/0.7880  =  c/0.8829

c  =  57.10(0.8829)

c  =  50.41

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.