USING AREA TO SOLVE PROBLEMS

We may need the area of different figures to solve many real-world problems. 

In this section, we are going to see, how area of figures can be used to solve real world problems.  

Example 1 :

A banquet room is being carpeted. A floor plan of the room is shown below. Each unit represents 1 yard. The carpet costs $23.50 per square yard. How much will it cost to carpet the room ?

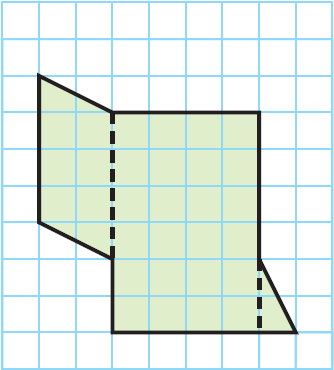
Solution :

Step 1 : 

Separate the composite figure into simpler shapes as shown by the dashed lines : a parallelogram, a rectangle, and a triangle.

Step 2 : 

Find the area the parallelogram. 

Base (b)  =  4 yards

Height (h)  =  2 yards

Use the formula.

A  =  bh

A  =  4 · 2

A  =  8 square yd

The area of the parallelogram is 8 square yards.

Step 3 : 

Find the area the rectangle. 

Length (l)  =  6 yards

Width (w)  =   4 yards

Use the formula.

A  =  lw

A  =  6 · 4

A  =  24 square yd

The area of the rectangle is 24 square yards.

Step 3 : 

Find the area the triangle. 

Base (b)  =  1 yard

Height (h)  =  2 yards

Use the formula.

A  =  (1/2) bh

A  =  (1/2)(1)(2)

A  =  1 square yd

The area of the triangle is 1 square yard.

Step 4 : 

Find the area of the composite figure.

A  =  8 + 24 + 1  =  33 square yards

Step 4 : 

Calculate the cost to carpet the room.

Total cost  =  Area · Cost per yard

Total cost  =  33 · $23.50

Total cost  =  $775.50

So, the cost to carpet the banquet room is $775.50.

Example 2 :

A window is being replaced with tinted glass. The plan at the right shows the design of the window. Each unit length represents 1 foot. The glass costs $28 per square foot. How much will it cost to replace the glass? Use 3.14 for π.

Solution : 

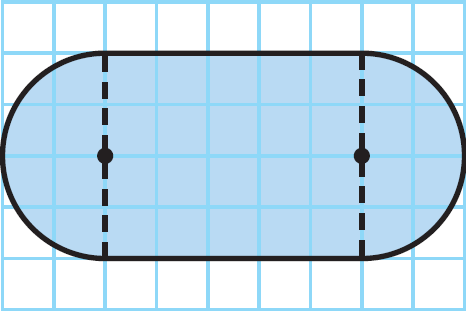
Solution :

Step 1 : 

Separate the composite figure into simpler shapes as shown by the dashed lines : a rectangle, two semicircles with equal area (one is one the left side of the rectangle and other one is on the right side).

Step 2 : 

Find the area the rectangle. 

Length (l)  =  5 ft

Width (w)  =   4 ft

Use the formula.

A  =  lw

A  =  5 · 4

A  =  20 square ft

The area of the rectangle is 24 square feet.

Step 3 : 

Find the combined area of two semi-circles. 

Radius  =  2 ft 

Use the formula.

A  =  2 x (1/2)πr²

A  =  πr²

A  =  (3.14)(2)²

A  =  (3.14)(4)

A  =  12.56 square ft

The combined area of two semi circles is about 12.56 square ft.

Step 4 : 

Find the area of the composite figure.

A  =  20 + 12.56  =  32.56 square ft

Step 5 : 

Calculate the cost of tinted glass for the window.

Total cost  =  Area · Cost per feet 

Total cost  =  32.56 · $28

Total cost  =  $911.68

So, the cost of tinted glass for the window is $911.68.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.