USING ADDITION TO SOLVE EQUATIONS

Example 1 :

Solve the following equation and graph the solution on a number line.

y - 21 = 18

Solution :

y - 21 = 18

Add 21 to both sides.

(y - 21) + 21 = 18 + 21

y - 21 + 21 = 39

y = 39

Example 2 :

Solve the following equation and graph the solution on a number line.

h - 1/2 = 3/4

Solution :

h - 1/2 = 3/4

Add 1/2 to both sides.

(h - 1/2) + 1/2 = 3/4 + 1/2

h - 1/2 + 1/2 = 3/4 + 2/4

h = (3 + 2)/4

h = 5/4

h = 1.25

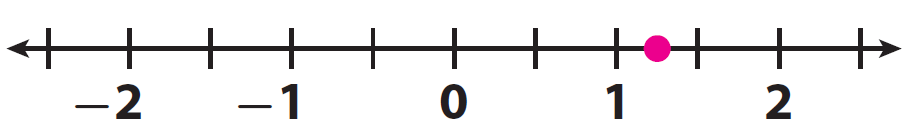
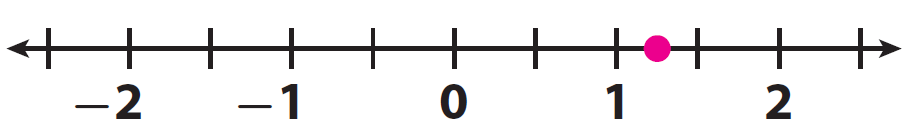
Example 3 :

Solve for x :

x - 7 = 8

Solution :

x - 7 = 8

Add 7 to both sides.

(x - 7) + 7 = 8 + 7

x - 7 + 7 = 15

x = 15

Example 4 :

Solve for a :

a - 3 = 11

Solution :

a - 3 = 11

Add 3 to both sides.

(a - 3) + 3 = 11 + 3

a - 3 + 3 = 14

a = 14

Example 5 :

When 7 is subtracted from a number, the result is 15. Find the number.

Solution :

Let x be the number.

x - 7 = 25

Add 7 to both sides.

(x - 7) + 7 = 15 + 7

x - 7 + 7 = 22

x = 22

Example 6 :

The difference between the two numbers is 22.5. If the smaller number is 7.5, find the larger number.

Solution :

Let x be the larger number.

x - 7.5  = 22.5

Add 7.5 to both sides.

(x - 7.5) + 7.5 = 22.5 + 7.5

x - 7.5 + 7.5 = 30

x = 30

The larger number is 30.

Example 7 :

Sarah used a gift card to buy $3 worth of food. She has $2 left on her gift card. Write an equation to represent this situation.

Model the equation and find how much money that she had initially in her gift card.

Solution :

Write a word equation based on the situation.

Rewrite the equation using a variable for the unknown quantity and the given values for the known quantities.

Let x be the amount on the card.

Then, we have

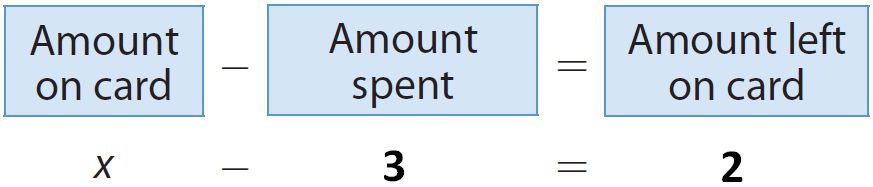
Therefore, the equation 'x - 3 = 2' represents the given situation.

Let us model the equation 'x - 3 = 2' using algebra tiles.

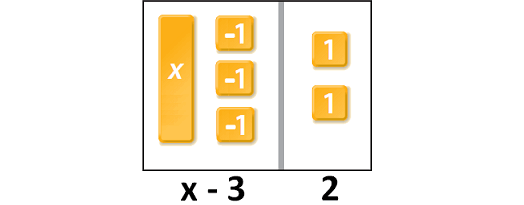
To find how much money that Sarah had initially, we have to solve for x.

To solve for x in the above model, we have to isolate x.

That is, we have to remove six '-1' tiles on the left side.

Whenever we remove '-1' tiles from one side of the mat, we must add the same number of '1' tiles on both sides.

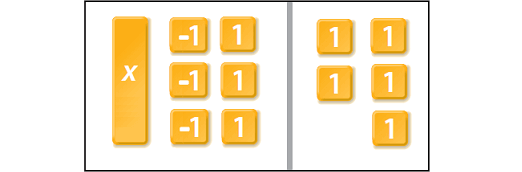
Cross out one '-1' tile for one '1' tile.

Then, we have

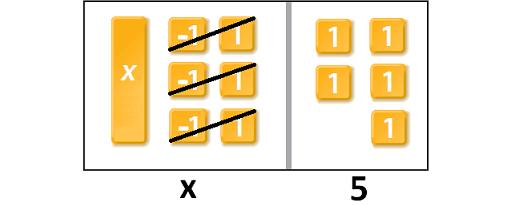
In the above model, we find x on the left side and five '1' tiles on the right side.

So, the value of x is 5.

Hence, Sarah had $5 initially in her gift card.

Example 8 :

Find the angle measure of polygon.

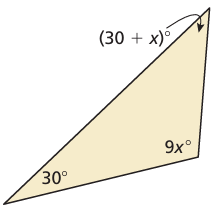
Solution :

Sum of interior angles of triangle = 180

30 + 9x + 30 + x = 180

10x + 60 = 180

10x = 180 - 60

10x = 120

x = 120/10

x = 12

Example 9 :

Use the table to find the number of miles x you need to bike on Friday so that the mean number of miles biked per day is 5.

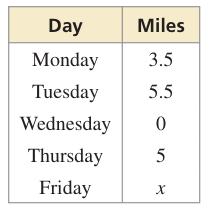
Solution :

Mean number of miles = 5

(3.5 + 5.5 + 0 + 5 + x)/5 = 5

(14 + x)/5 = 5

14 + x = 5(5)

14 + x = 25

x = 25 - 14

x = 11

So, the missing value of x is 11.

Example 10 :

The formula d = (1/2)  n + 26 relates the nozzle pressure n (in pounds per square inch) of a fire hose and the maximum horizontal distance the water reaches d (in feet). How much pressure is needed to reach a fire 50 feet away?

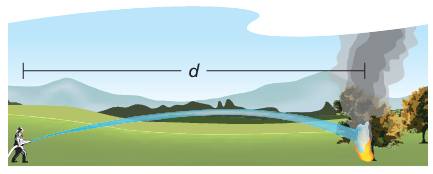
Solution :

Distance to be reached = 50 ft

d = (1/2)  n + 26

50 = (1/2)  n + 26

50 - 26 = (1/2) n

24 = (1/2)n

n = 24 (2)

n = 48

So, the required pressure is 48 pounds per square inch.

Example 11 :

Your school’s drama club charges $4 per person for admission to a play. The club borrowed $400 to pay for costumes and props. After paying back the loan, the club has a profit of $100. How many people attended the play?

Solution :

Let x be the number of people attended the play.

Admission charge = $4

Amount borrowed = $400

Ticket price ⋅ (Number of people who attended) − Amount of loan = Profi t

4x - 400 = 100

4x = 100 + 400

4x = 500

x = 500/4

x = 125

So, the number of people is 125.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.