TRIGONOMETRY WORD PROBLEMS WITH SOLUTIONS
Problem 1 :
The angle of elevation of the top of the building at a distance of 50 m from its foot on a horizontal plane is found to be 60°. Find the height of the building.
Solution :
Draw a sketch.
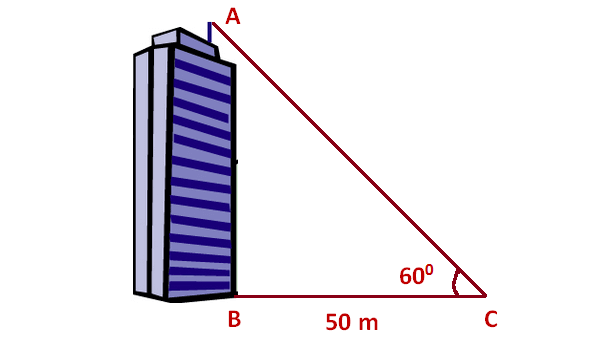
Here, AB represents height of the building, BC represents distance of the building from the point of observation.
In the right triangle ABC, the side which is opposite to the angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and the remaining side is called adjacent side (BC).
Now we need to find the length of the side AB.
tanθ = Opposite side/Adjacent side
tan60° = AB/BC
√3 = AB/50
√3 x 50 = AB
AB = 50√3
Approximate value of √3 is 1.732
AB = 50 (1.732)
AB = 86.6 m
So, the height of the building is 86.6 m.
Problem 2 :
A ladder placed against a wall such that it reaches the top of the wall of height 6 m and the ladder is inclined at an angle of 60°. Find how far the ladder is from the foot of the wall.
Solution :
Draw a sketch.
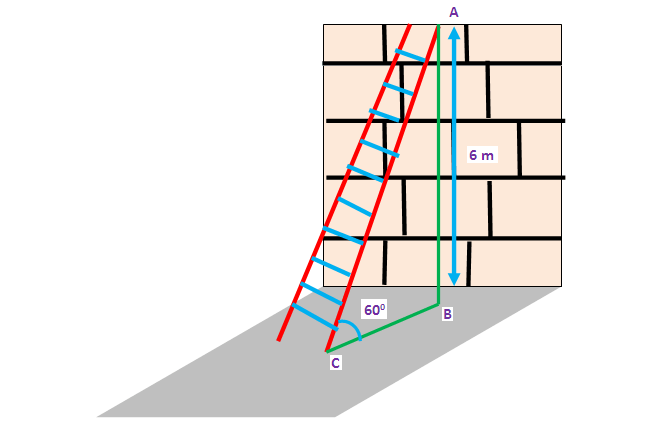
Here AB represents height of the wall, BC represents the distance between the wall and the foot of the ladder and AC represents the length of the ladder.
In the right triangle ABC, the side which is opposite to angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now, we need to find the distance between foot of the ladder and the wall. That is, we have to find the length of BC.
tanθ = opposite side/adjacent side
tan60° = AB/BC
√3 = 6/BC
BC = 6/√3
BC = (6/√3) x (√3/√3)
BC = (6√3)/3
BC = 2√3
Approximate value of √3 is 1.732.
BC = 2 (1.732)
BC = 3.464 m
So, the distance between foot of the ladder and the wall is 3.464 m.
Problem 3 :
A string of a kite is 100 meters long and the inclination of the string with the ground is 60°. Find the height of the kite, assuming that there is no slack in the string.
Solution :
Draw a sketch.
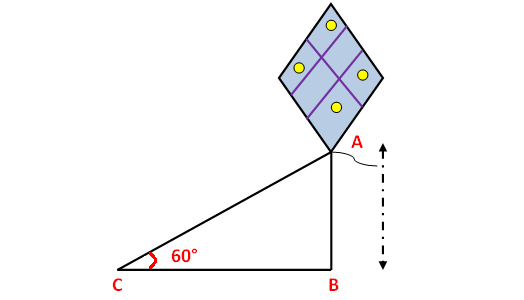
Here AB represents height of kite from the ground, BC represents the distance of kite from the point of observation.
In the right triangle ABC the side which is opposite to angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the height of the side AB.
sinθ = opposite side/hypotenuse side
sinθ = AB/AC
sin60° = AB/100
√3/2 = AB/100
(√3/2) x 100 = AB
AB = 50√3 m
So, the height of kite from the ground 50√3 m.
Problem 4 :
From the top of the tower 30 m height a man is observing the base of a tree at an angle of depression measuring 30°. Find the distance between the tree and the tower.
Solution :
Draw a sketch.
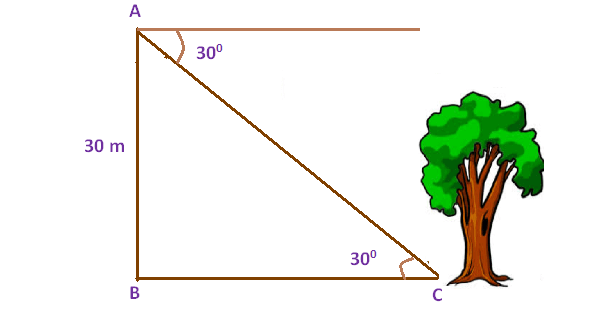
Here AB represents height of the tower, BC represents the distance between foot of the tower and the foot of the tree.
Now we need to find the distance between foot of the tower and the foot of the tree (BC).
tanθ = opposite side/adjacent side
tan30° = AB/BC
1/√3 = 30/BC
BC = 30√3
Approximate value of √3 is 1.732.
BC = 30(1.732)
BC = 51.96 m
So, the distance between the tree and the tower is 51.96 m.
Problem 5 :
A man wants to determine the height of a light house. He measured the angle at A and found that tan A = 3/4. What is the height of the light house if A is 40m from the base?
Solution :
Draw a sketch.
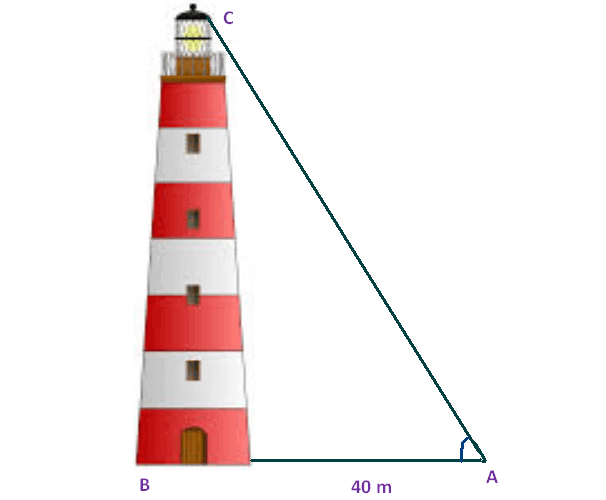
Here BC represents height of the light house, AB represents the distance between the light house from the point of observation.
In the right triangle ABC the side which is opposite to the angle A is known as opposite side (BC), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (AB).
Now we need to find the height of the light house (BC).
tanA = opposite side/adjacent side
tanA = BC/AB
Given : tanA = 3/4.
3/4 = BC/40
Multiply each side by 40.
30 = BC
So, the height of the light house is 30 m.
Problem 6 :
A ladder is leaning against a vertical wall makes an angle of 20° with the ground. The foot of the ladder is 3 m from the wall. Find the length of ladder.
Solution :
Draw a sketch.
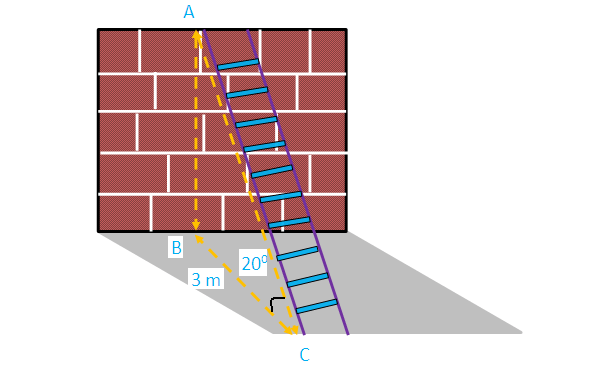
Here AB represents height of the wall, BC represents the distance of the wall from the foot of the ladder.
In the right triangle ABC, the side which is opposite to the angle 20° is known as opposite side (AB),the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the length of the ladder (AC).
cosθ = adjacent side/hypotenuse side
Cosθ = BC/AC
Cos 20° = 3/AC
0.9397 = 3/AC
AC = 3/0.9396
AC = 3.192
So, the length of the ladder is about 3.193 m.
Problem 7 :
A kite is flying at a height of 65 m attached to a string. If the inclination of the string with the ground is 31°, find the length of string.
Solution :
Draw a sketch.
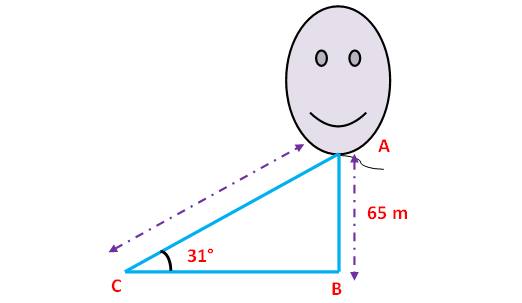
Here AB represents height of the kite. In the right triangle ABC the side which is opposite to angle 31° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and the remaining side is called adjacent side (BC).
Now we need to find the length of the string AC.
sinθ = opposite side/hypotenuse side
sinθ = AB/AC
sin31° = AB/AC
0.5150 = 65/AC
AC = 65/0.5150
AC = 126.2 m
Hence, the length of the string is 126.2 m.
Problem 8 :
The length of a string between a kite and a point on the ground is 90 m. If the string makes an angle θ with the ground level such that tan θ = 15/8, how high will the kite be ?
Solution :
Draw a sketch.
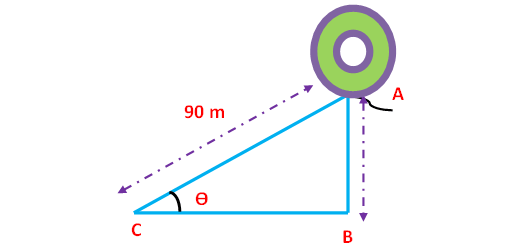
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle θ is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the length of the side AB.
tanθ = 15/8 ----> cotθ = 8/15
cscθ = √(1+ cot2θ)
cscθ = √(1 + 64/225)
cscθ = √(225 + 64)/225
cscθ = √289/225
cscθ = 17/15 ----> sinθ = 15/17
But, sinθ = opposite side/hypotenuse side = AB/AC.
AB/AC = 15/17
AB/90 = 15/17
AB = 79.41
So, the height of the tower is 79.41 m.
Problem 9 :
An airplane is observed to be approaching a point that is at a distance of 12 km from the point of observation and makes an angle of elevation of 50°. Find the height of the airplane above the ground.
Solution :
Draw a sketch.
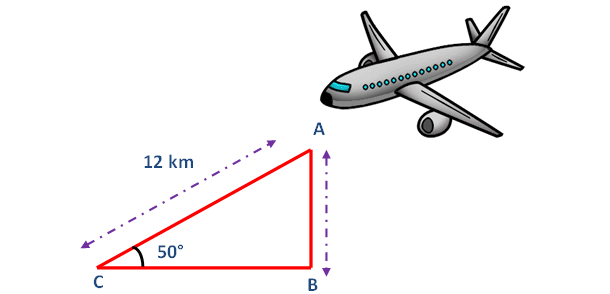
Here AB represents height of the airplane from the ground. In the right triangle ABC the side which is opposite to angle 50° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the length of the side AB.
From the figure given above, AB stands for the height of the airplane above the ground.
sinθ = opposite side/hypotenuse side
sin50° = AB/AC
0.7660 = h/12
0.7660 x 12 = h
h = 9.192
So, the height of the airplane above the ground is 9.192 km.
Problem 10 :
A balloon is connected to a meteorological station by a cable of length 200 m inclined at 60° angle with the ground. Find the height of the balloon from the ground. (Imagine that there is no slack in the cable)
Solution :
Draw a sketch.
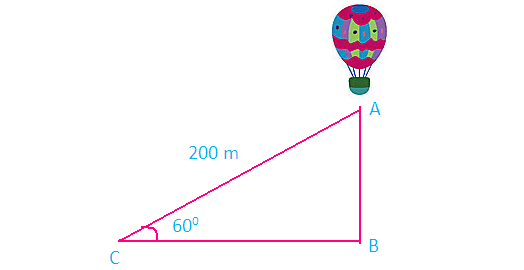
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse (AC) and the remaining side is called as adjacent side (BC).
Now we need to find the length of the side AB.
From the figure given above, AB stands for the height of the balloon above the ground.
sinθ = opposite side/hypotenuse side
sinθ = AB/AC
sin60° = AB/200
√3/2 = AB/200
AB = (√3/2) x 200
AB = 100√3
AB = 100(1.732)
AB = 173.2 m
So, the height of the balloon from the ground is 173.2 m.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 28)
Oct 14, 25 10:57 AM
10 Hard SAT Math Questions (Part - 28) -
SAT Math Questions and Answers
Oct 13, 25 01:09 PM
SAT Math Questions and Answers -
10 Hard SAT Math Questions (Part - 27)
Oct 13, 25 11:55 AM
10 Hard SAT Math Questions (Part - 27)