SAT MATH QUESTIONS AND ANSWERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Rajesh sells only hats and scarves at his store, for which he charges $13 and $7, respectively. On Monday, he sold 15 items and made $123. How many hats did Rajesh sell on Monday?
(A) 3
(B) 4
(C) 5
(D) 6
Answer :
Let h be the number of hats and s be the number of scarves sold on Monday.
h + s = 15 ----(1)
13h + 7s = 123 ----(2)
Solve (1) for s.
h + s = 15
s = 15 - h
Substitute s = 15 - h into (2).
13h + 7(15 - h) = 123
13h + 105 - 7h = 123
6h + 105 = 123
6h = 18
h = 3
Rajesh sold 3 hats on Monday.
Therefore, the correct answer choice is (A).
Question 2 :
From where he lives, it costs Jared $4 more for a roundtrip train ticket to Chaska than it does for one to Waconia. Last month, Jared took roundtrips to Chaska 7 times and to Waconia 8 times. If he spent a total of $103 on train tickets, how much does Jared spend on one roundtrip ticket to Waconia?
(A) $12
(B) $10
(C) $7
(D) $5
Answer :
Let x be the cost for a roundtrip train ticket to Waconia
Then the the cost for a roundtrip train ticket to Chaska is (x + 4).
7(x + 4) + 8x = 103
7x + 28 + 8x = 103
15x + 28 = 103
15x = 75
x = 5
Jared spends $5 on one roundtrip ticket to Waconia
Therefore, the correct answer choice is (D).
Question 3 :
The function f is defined by f(x) = ax2 + bx + c, where a, b and c are constants. The graph of y = f(x) in the xy-plane passes through the points (13, 0) and (-6, 0). Which of the following is the value of a + b in terms of a?
A) 7a
B) 6a
C) -6a
D) -7a
Answer :
Since the given quadratic function f(x) = ax2 + bx + c is in standard form, we can use the formula given below to find the x-coordinate of the vertex.
x = -b/2a ----(1)
Given : The graph of y = f(x) in the xy-plane passes through the points (13, 0) and (-6, 0).
Since the y-coordinate is 0 in the given two points, they represent x-intercepts. And also, average of the x-coordinates of the two x-intercepts is equal to x-coordinate of the vertex.
Average of x-coordinates = (13 - 6)/2
= 7/2
= 3.5
Substitutr x = 3.5 in (1).
3.5 = -b/2a
Multiply both sides by -2a.
-7a = b
Now, substitutr b = 7a in the expression a + b.
a + b = a - 7a
a + b = -6a
The correct answer choice for this question is (C).
Question 4 :
3x + 2y = 15
5x - y = 12
Which of the following ordered pairs (x, y) satisfies the system of equations above?
(A) (3, 3)
(B) (2, 3)
(C) (4, 8)
(D) (5, 0)
Answer :
3x + 2y = 15 ----(1)
5x - y = 12 ----(2)
x = 3
Substitute x = 3 into (2).
5(3) - y = 12
15 - y = 12
-y = -3
y = 3
Solution :
(x, y) = (3, 3)
Therefore, the correct answer choice is (A).
Question 5 :
12 - 13x > ⁽ˣ ⁺ ¹⁾⁄₍ₓ ₋ ₉₎
Which of the following numbers is a solution to the inequality above?
(A) 5
(B) 3
(C) 1
(D) 0
Answer :
Instead of solving the given inequality, it is easier to check each of the given answer choices with the given inequality.
Option (A) :
Substitute x = 5.
12 - 13(5) > ⁽⁵ ⁺ ¹⁾⁄₍₅ ₋ ₉₎
-53 > -1.5
(false)
Option (A) :
Substitute x = 3.
12 - 13(3) > ⁽² ⁺ ¹⁾⁄₍₂ ₋ ₉₎
-27 > -0.43
(false)
Option (C) :
Substitute x = 1.
12 - 13(1) > ⁽¹ ⁺ ¹⁾⁄₍₁ ₋ ₉₎
-1 > -0.125
(false)
Option (D) :
Substitute x = 0
12 - 13(0) > ⁽⁰ ⁺ ¹⁾⁄₍₀ ₋ ₉₎
12 > -¹⁄₉
(true)
Therefore, the correct answer choice is (D).
Question 6 :
The audience of a reality TV show cast a total of 3.4 million votes and each vote went to either Brian or Susan. If Susan received 34,000 more votes than Brian, what percent of votes were cast for Brian?
(A) 45%
(B) 49%
(C) 49.5%
(D) 49.9%
Answer :
Let x be the number of votes received by Brian.
Then, Susan received (x + 34,000) votes.
Given : Total number of votes is 3.4 million.
x + (x + 34,000) = 34,00,000
x + x + 34,000 = 34,00,000
2x + 34,000 = 34,00,000
2x = 33,66,000
x = 16,83,000
Number of votes received by Brian = 16,83,000
Percent of votes were cast for Brian :
= 49.5%
Therefore, the correct answer choice is (C).
Question 7 :
Marisol has two different methods of commuting to and from work : she either takes the subway, which costs $2.75 per one-way trip, or she takes a car service, which costs $18.50 per one-way trip. Last week, she worked 5 days, commuting to and from work each day. If her total commuting cost for the week was $74.75, how many times did she take the car service?
(A) 2
(B) 3
(C) 4
(D) 6
Answer :
Last week she worked 5 days, commuting to and from work each day.
Total number of one-way trip :
= 2(5)
= 10
Let x be the number one-way trip in subway and y be the number of one-way trip in car service.
x + y = 10 ----(1)
2.75x + 18.5y = 74.75 ----(2)
Solve for x in (1).
x + y = 10
x = 10 - y
Substitute x = 10 - y into (2).
2.75(10 - y) + 18.5y = 74.75
27.5 - 2.75y + 18.5y = 74.75
27.5 - 2.75y + 18.5y = 74.75
15.75y + 27.5 = 74.75
15.75y = 47.25
y = 3
The number of one-way trip, Marisol takes car service is 3.
Therefore, the correct answer choice is (B).
Question 8 :
V(n) = 8100(⁷⁄₆)n
A number of years ago, Andy purchased $8,100 worth of stock in PGHH Corporation. The value, in dollars, of his stock n years after purchase is given by the function V, above. If the stock is worth 11,000 now, roughly how many years ago did Andy purchase his stock?
(A) Five
(B) Four
(C) Three
(D) Two
Answer :
V(5) = 8100(⁷⁄₆)5
V(5) = 8100(1.17)n
It is easier to tolve this problem by checking the given answer choices.
Option (A) :
Substitute n = 5 into the given function.
V(5) = 8100(1.17)5
V(5) ≈ 17,759
Option (B) :
Substitute n = 4 into the given function.
V(4) = 8100(1.17)4
V(4) ≈ 15,178
Option (C) :
Substitute n = 3 into the given function.
V(4) = 8100(1.17)3
V(4) ≈ 12,973
Option (D) :
Substitute n = 2 into the given function.
V(2) = 8100(1.17)2
V(2) ≈ 11,088
The value of V(2) is close to $11,000.
Therefore, the correct answer choice is (D).
Question 9 :
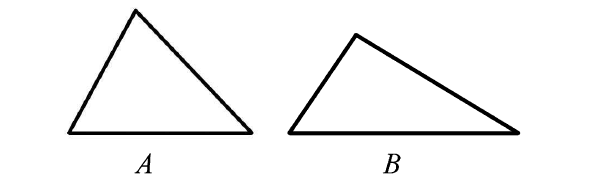
The two triangles in the figure above, labeled A and B, each have the same area. The base of triangle B is p percent longer than the base of triangle A, and the height of triangle B is r percent less than the height of triangle A. If p - r = 5, which of the following could be the value of p ?
(A) 15
(B) 18
(C) 23
(D) 25
Answer :
Let the base and height of triangle A be 100 each.
Area of triangle = (½)base ⋅ height
Area of triangle A :
= (½)100 ⋅ 100
= 5000
From the given information,
base of triangle B = 100 + p
height of triangle B = 100 - r
Area of triangle B :
= (½)(100 + p) ⋅ (100 - r)
Given : Both the triangles have the same area.
(½)(100 + p) ⋅ (100 - r) = 5000
(100 + p)(100 - r) = 10000
10000 - 100r + 100p - pr = 10000
100p - 100r - pr = 0
100(p - r) - pr = 0
Substitute p - r = 5
100(5) - pr = 0
500 - pr = 0
pr = 500
Since p - r = 5, r = p - 5.
p(p - 5) = 500
p2 - 5p = 500
p2 - 5p - 500 = 0
p2 - 25p + 20p - 500 = 0
p(p - 25) + 20(p - 25) = 0
(p - 25)(p + 20) = 0
p - 25 = 0 or p + 20 = 0
p = 25 or p = -20
We can ignore the ngative value of p. So, p = 25
Therefore, the correct answer choice is (D).
Question 10 :
In the xy-plane, a line containing the points (a, a3) and (10, 40) passes through the origin. Which of the following could be the value of a?
(A) -3
(B) -2
(C) 3
(D) 4
Answer :
The given line passes through the following three points.
(a, a3), (10, 40), (0, 0)
Formula to find the slope of a line joining two points :
Substitute (x1, y1) = (a, a3) and (x2, y2) = (10, 40) to get the slope of the given line.
Substitute (x1, y1) = (10, 40) and (x2, y2) = (0, 0) to get the slope of the given line.
Both (1) and (2) give the slope of the given line.
40 - a3 = 4(10 - a)
40 - a3 = 40 - 4a
-a3 = -4a
a3 = 4a
a3 - 4a = 0
a = 0 or a2 - 4 = 0
Solve a2 - 4 = 0.
a2 - 4 = 0
a2 - 22 = 0
(a + 2)(a - 2) = 0
a = -2 or a = 2
We get three values for a
a = -2, 0, 2
We have -2 in the answer choice (B).
Therefore, the correct answer choice is (B).
You might like these
Solving the HARDEST SAT Math Questions ONLY using Desmos
Tricky SAT Math Problems Solved Easily
10 Hard Digital SAT Math Questions (Part - 1)
10 Hard Digital SAT Math Questions (Part - 2)
10 Hard Digital SAT Math Questions (Part - 3)
10 Hard Digital SAT Math Questions (Part - 4)
10 Hard Digital SAT Math Questions (Part - 5)
10 Hard Digital SAT Math Questions (Part - 6)
10 Hard Digital SAT Math Questions (Part - 7)
10 Hard Digital SAT Math Questions (Part - 8)
10 Hard Digital SAT Math Questions (Part - 9)
10 Hard Digital SAT Math Questions (Part - 10)
10 Hard Digital SAT Math Questions (Part - 11)
10 Hard Digital SAT Math Questions (Part - 12)
10 Hard Digital SAT Math Questions (Part - 13)
10 Hard Digital SAT Math Questions (Part - 14)
10 Hard Digital SAT Math Questions (Part - 15)
10 Hard Digital SAT Math Questions (Part - 16)
10 Hard Digital SAT Math Questions (Part - 17)
10 Hard Digital SAT Math Questions (Part - 18)
10 Hard Digital SAT Math Questions (Part - 19)
10 Hard Digital SAT Math Questions (Part - 20)
10 Hard Digital SAT Math Questions (Part - 21)
10 Hard Digital SAT Math Questions (Part - 22)
10 Hard Digital SAT Math Questions (Part - 23)
10 Hard Digital SAT Math Questions (Part - 24)
10 Hard Digital SAT Math Questions (Part - 25)
10 Hard Digital SAT Math Questions (Part - 26)
10 Hard Digital SAT Math Questions (Part - 27)
10 Hard Digital SAT Math Questions (Part - 28)
10 Hard Digital SAT Math Questions (Part - 29)
10 Hard Digital SAT Math Questions (Part - 30)
10 Hard Digital SAT Math Questions (Part - 31)
10 Hard Digital SAT Math Questions (Part - 32)
10 Hard Digital SAT Math Questions (Part - 33)
10 Hard Digital SAT Math Questions (Part - 34)
10 Hard Digital SAT Math Questions (Part - 35)
10 Hard Digital SAT Math Questions (Part - 36)
10 Hard Digital SAT Math Questions (Part - 37)
10 Hard Digital SAT Math Questions (Part - 38)
10 Hard Digital SAT Math Questions (Part - 39)
10 Hard Digital SAT Math Questions (Part - 40)
10 Hard Digital SAT Math Questions (Part - 41)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 41)
Dec 28, 25 06:05 PM
10 Hard SAT Math Questions (Part - 41)

