TRIGONOMETRY PROBLEMS INVOLVING ANGLE OF DEPRESSION

Angle of Depression :

The angle of depression is an angle formed by the line of sight with the horizontal when the point is below the horizontal level. That is, the case when we lower our head to look at the point being viewed.

To find questions 1 to 3, please visit the page "Trigonometry Word Problems with Angle of Depression"

Practice Questions

Question 1 :

An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. (√3 = 1.732)

Solution :

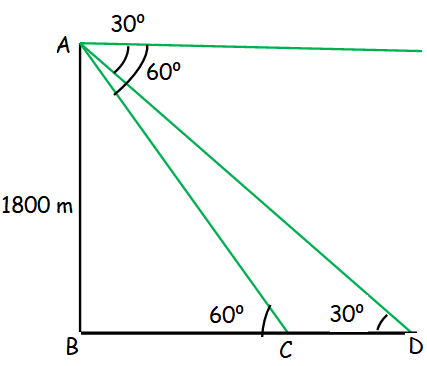
In triangle ABC,

tan θ  =  Opposite side / Adjacent side 

tan 60  =  AB/BC

√3  =  1800/BC

BC  =  1800/√3

BC  =  600√3

In triangle ABD,

tan 30  =  AB / BD

1/√3   =  1800/ BD

BD  =  1800√3

Distance between two boats  =  CD

  =  BD - BC

  =  1800√3 -  600√3

  =  1200 √3

=  1200(1.732)

Distance between two boats  =  2078.4 m

Question 2 :

From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it are observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is 4h/√3 m.

Solution :

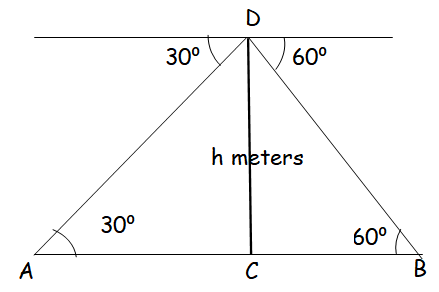
In triangle ADC,

tan 30  =  DC/AC

1/√3  =  h/AC

AC  =  √3 h -----(1)

In triangle DCB,

tan 60  =  DC/BC

√3  =  h/BC

BC  =  h/√3 -----(2)

(1) + (2)

AC + BC  =  √3 h + (h/√3)

Distance between two ships  =  (3h + h)/√3

Distance between two ships  =  4h/√3

Hence proved.

Question 3 :

A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is 30√3 feet from the entrance of the lift, find the speed in ft/sec of the lift which is descending.

Solution :

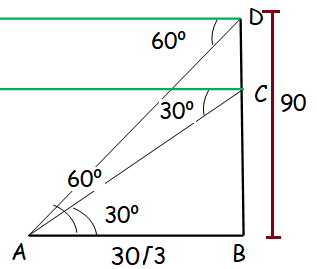
In the diagram above, in the right triangle ABC,

tan30°  =  opposite side / adjacent side

1/√3  =  BC/30√3

30  =  BC

DC  =  DB - CB

DC  =  90 - 30

DC  =  60 feet

So, the left has descended 60 ft in 2 minutes.

Speed  =  Distance / Time

Speed  =  60/2

Speed  =  30 ft/min

Speed  =  30 ft/(60 seconds)

Speed  =  30/60 ft/sec

Speed  =  0.5 ft/sec

So, the speed of the lift which is descending is 0.5 ft/sec.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.