TRIGONOMETRY WORD PROBLEMS WITH ANGLE OF DEPRESSION

Angle of Depression :

The angle of depression is an angle formed by the line of sight with the horizontal when the point is below the horizontal level. That is, the case when we lower our head to look at the point being viewed.

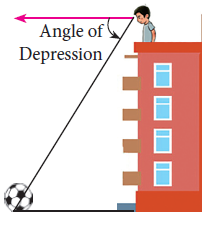
Problems

Problem 1 :

From the top of a rock 50√3 m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock.

Solution :

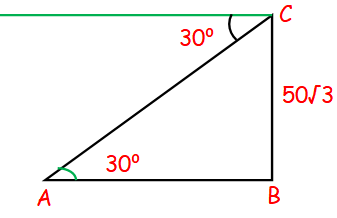
BC = Rock, 

Car in the position A.

tan θ  =  Opposite side / Adjacent side 

tan 30  =  BC/AB

1/√3  =  50√3/AB

AB  =  50√3(√3)

AB  =  50(3)

AB  =  150 m

The distance of the car from the rock is 150 m.

Problem 2 :

The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building.

Solution :

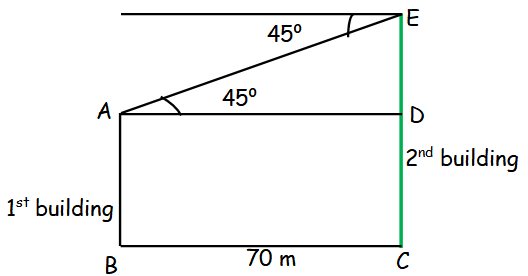
CE  =  120 m

Let DC = x

BC   =  DC  =  70 m

In triangle ADE,

tan 45  =  DE/AD

1  =  (120 - x)/70

70  =  120 - x

x  =  120 - 70

x  =  50 m

So, the height of the 1^st building is 50 m

Problem 3 :

From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post. (tan 38° = 0.7813, √3 = 1.732)

Solution :

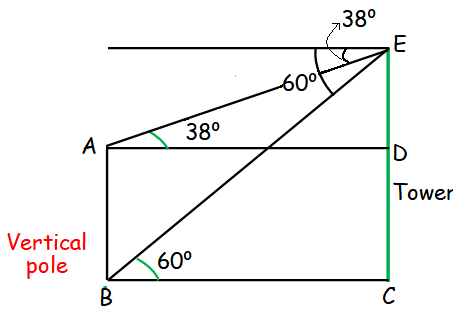
Height of tower  =  60 m

Let DC = x, ED  =  60 - x

In triangle ADE,

tan 38  =  DE/AD

0.7813  =  (60 - x)/AD

AD  =  (60 - x)/ 0.7813 ---(1)

In triangle BEC,

tan 60  =  EC/BC

√3  =  60/BC

BC  =  60/√3 

BC  =  20√3 ------(2)

(1)  =  (2)

(60 - x)/0.7813  =  20√3

60 - x  =  20(0.7813)(1.732)

60 - x  =  34.64(0.7813)

60 - x  =  27.06

x  =  60 - 27.06

x  =  32.94

So, the height of the vertical lamp post is 32.94 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.