TIME SPEED AND DISTANCE PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
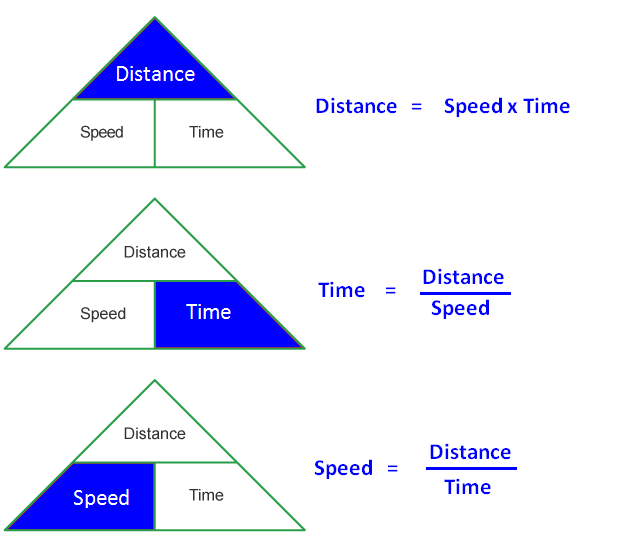
Formulas
To know the shortcuts required to solve problems on time, speed and distance,
Problem 1 :
If a person drives his car in the speed 50 miles per hour, how far can he cover in 2.5 hours?
Solution :
Given : Speed is 50 miles per hour.
So, the distance covered in 1 hour is
= 50 miles
Then, the distance covered in 2.5 hours is
= 2.5 ⋅ 50 miles
= 125 miles
So, the person can cover 125 miles of distance in 2.5 hours.
Problem 2 :
If a person travels at a speed of 40 miles per hour. At the same rate, how long will he take to cover 160 miles distance?
Solution :
Given : Speed is 40 miles per hour.
The formula to find the time when distance and speed are given is
Time taken to cover the distance of 160 miles is
= ¹⁶⁰⁄₄₀
= 4 hours
So, the person will take 4 hours to cover 160 miles distance at the rate of 40 miles per hour.
Problem 3 :
A person travels at a speed of 60 miles per hour. How far will he travel in 4.5 hours?
Solution :
Given : Speed is 60 miles per hour.
The distance covered in 1 hour is
= 60 miles
Then, the distance covered in 4.5 hours is
= 4.5 ⋅ 60 miles
= 270 miles
So, the person will travel 270 miles distance in 4.5 hours.
Problem 4 :
A person travels at a speed of 60 kms per hour. Then how many meters can he travel in 5 minutes?
Solution :
Given : Speed is 60 kms per hour.
The distance covered in 1 hour or 60 minutes is
= 60 kms
= 60 ⋅ 1000 meters
= 60000 meters
Then the distance covered in 1 minute is
= 60000/60
= 1000 m
The distance covered in 5 minutes is
= 5 ⋅ 1000
= 5000 meters
So, the person can cover 5000 meters distance in 5 minutes.
Problem 5 :
A person covers 108 kms in 3 hours. What is his speed in meter per second?
Solution :
Given : Distance is 108 kms and time is 3 hours.
The given distance in meters :
= 108 ⋅ 1000
= 108,000 meters
The given time in seconds :
= 3 ⋅ 60 minutes
= 180 minutes
= 180 ⋅ 60 seconds
= 10,800 seconds
The formula to find the speed is
Speed in meter per second is
= ¹⁰⁸⁰⁰⁰⁄₁₀₈₀₀
= 10 m/sec
So, his speed in meter per second is 10.
Problem 6 :
A person covers 90 kms in 2 hours 30 minutes. Find the speed in meter per second.
Solution :
Given : Distance is 90 kms and time is 2 hrs 30 min.
The given distance in meters :
= 90 ⋅ 1000
= 90,000 meters
The given time in seconds :
= 2 hrs 30 min
= (120 + 30) min
= 150 minutes
= 150 ⋅ 60 seconds
= 9,000 seconds
The formula to find the speed is
Speed in meter per second is
= ⁹⁰⁰⁰⁰⁄₉₀₀₀
= 10 m/sec
So, his speed in meter per second is 10.
Problem 7 :
A person travels at the rate of 60 miles per hour and covers 300 miles in 5 hours. If he reduces his speed by 10 miles per hour, how long will he take to cover the same distance?
Solution :
Original speed is 60 miles per hour.
If the speed is reduced by 10 miles per hour, then the new speed is
= 50 miles per hour
Distance to be covered is 300 miles.
The formula to find time is
Time taken to cover 300 miles distance at the speed of 50 miles per hour is
= ³⁰⁰⁄₅₀
= 6 hours
So, if the person reduces his speed by 10 miles per hour, he will take 6 hours to cover 300 miles distance.
Problem 8 :
A person travels 50 kms per hour. If he increases his speed by 10 kms per hour, how many minutes will he take to cover 8000 meters?
Solution :
Original speed is 50 kms per hour.
If the speed is increased by 10 kms per hour, then the new speed is
= 60 kms per hour
Because, we have to find the time in minutes for the distance given in meters, let us change the speed from kms per hour into meters per minute.
1 hour ----> 60 kms
1 ⋅ 60 minutes ----> 60 ⋅ 1000 meters
60 minutes ----> 60000 meters
1 minute ----> ⁶⁰⁰⁰⁰⁄₆₀ meters
1 minute ----> 1000 meters
So, the speed is 1000 meters/minute.
The formula to find time is
Time = Distance/Speed
Time taken to cover 8000 meters distance at the speed of 1000 meters per minute is
= ⁸⁰⁰⁰⁄₁₀₀₀
= 8 minutes
So, if the person increases his speed by 10 kms per hour, he will take 8 minutes to cover 8000 meters distance.
Problem 9 :
A person can travel at the speed of 40 miles per hour. If the speed is increased by 50%, how long will it take to cover 330 miles?
Solution :
Original speed is 40 miles per hour.
If the speed is increased by 50%, then the new speed is
= 150% of 40
= 1.5 ⋅ 40
= 60 miles per hour
Distance to be covered is 330 miles.
The formula to find time is
Time taken to cover 330 miles distance at the speed of 60 miles per hour is
= ³³⁰⁄₆₀
= 5.5 hours
= 5 hrs 30 minutes
So, if the person is increased by 50%, it will take 5 hrs 30 minutes to cover 330 miles distance.
Problem 10 :
A person speed at a rate of 40 kms per hour. If he increases his speed by 20%, what is his new speed in meter per minute?
Solution :
Original speed is 40 kms per hour
If the speed is increased by 20%, then the new speed is
= 120 % of 40
= 1.2 ⋅ 40
= 48 kms per hour
Now, let us change the speed from kms per hour into meters per minute.
1 hour ----> 48 kms
1 ⋅ 60 minutes ----> 48 ⋅ 1000 meters
60 minutes ----> 48,000 meters
1 minute ----> ⁴⁸⁰⁰⁰⁄₆₀ meters
1 minute ----> 800 meters
So, the speed is 800 meters/minute.
If the person increases his speed by 20%, his new speed will be 800 meter per minute.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 23)
Feb 27, 26 04:01 AM
Digital SAT Math Problems and Solutions (Part - 23) -
Digital SAT Math Problems and Solutions (Part - 22)
Feb 26, 26 08:43 PM
Digital SAT Math Problems and Solutions (Part - 22) -
10 Tricky SAT Math Questions with Answers
Feb 25, 26 08:07 AM
10 Tricky SAT Math Questions with Answers