SURFACE AREA OF PYRAMIDS AND CONES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Finding the Surface Area of a Pyramid
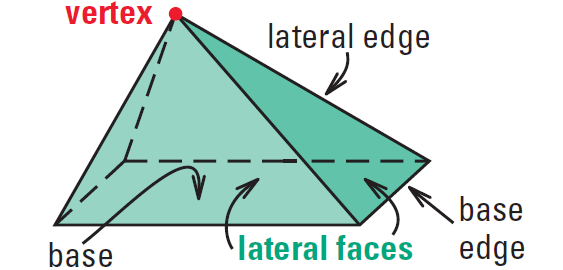
A pyramid is a polyhedron in which the base is a polygon and the lateral faces are triangles with a common vertex. The intersection of two lateral faces is a lateral edge. The intersection of the base and a lateral face is a base edge. The altitude, or height, of the pyramid is the perpendicular distance between the base and the vertex.
Pyramid :
Regular Pyramid :
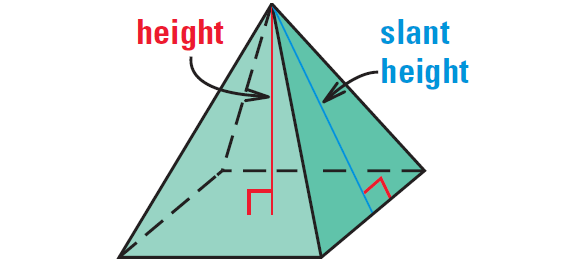
A regular pyramid has a regular polygon for a base and its height meets the base at its center. The slant height of a regular pyramid is the altitude of any lateral face. A non-regular pyramid does not have a slant height.
A regular hexagonal pyramid and its net are shown below. Let b represent the length of a base edge, and let l represent the slant height of the pyramid.
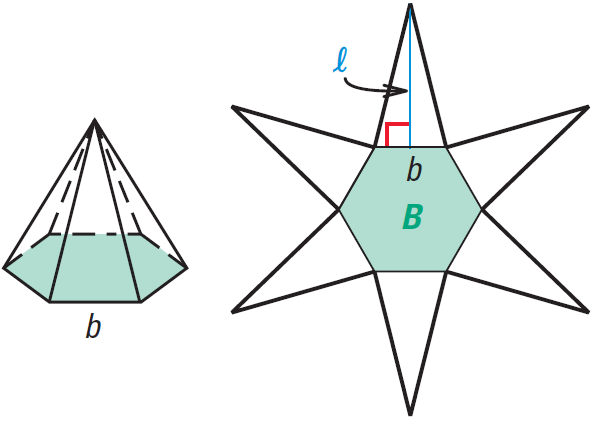
The area of each lateral face is
= 1/2 ⋅ bl
and the perimeter of the base is
P = 6b
So, the surface area is a s follows :
S = (Area of the base) + 6(Area of lateral surface)
Substitute.
S = B + 6(1/2 ⋅ bl)
Rewrite 6(1/2 ⋅ bl) as 1/2 ⋅ (6b)l.
S = B + 1/2 ⋅ (6b)l
Substitute P for 6b.
S = B + 1/2 ⋅ Pl
Surface Area of a Regular Pyramid
Theorem :
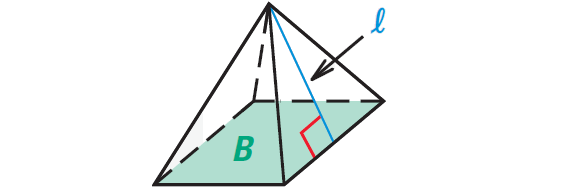
The surface area S of a regular pyramid is
S = B + 1/2 ⋅ Pl
where B is the area of the base, P is the perimeter of the base, and l is the slant height.
Finding the Surface Area of a Cone
A circular cone or cone has a circular base and a vertex that is not in the same plane as the base. The altitude, or height, is the perpendicular distance between the vertex and the base.
In a right cone shown below, the height meets the base at its center and the slant height is the distance between the vertex and a point on the base edge.
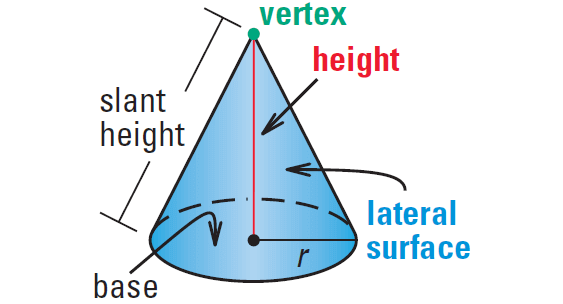
The lateral surface of a cone consists of all segments that connect the vertex with points on the base edge. When we cut along the slant height and lie the cone flat, we get the net shown below.
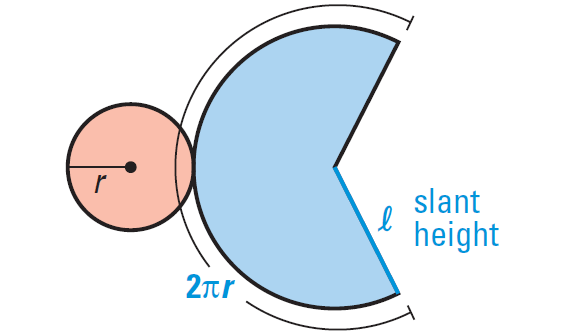
In the net, the circular base has an area of πr2 and the lateral surface is the sector of a circle. We can find the area of this sector by using a proportion, as shown below.
Set up proportion :

Area of sector/πl2 = 2πr/2πl
Area of sector/πl2 = r/l
Multiply each side by πl2.
Area of sector = πl2 ⋅ (r/l)
Simplify.
Area of sector = πrl
The surface area of a cone is the sum of the base area and the lateral area, πrl.
Theorem :
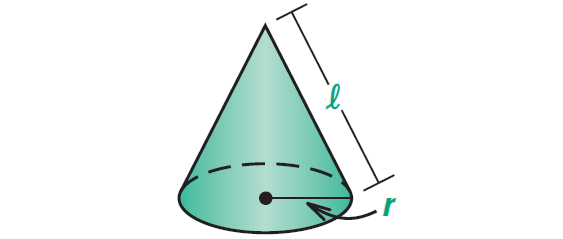
The surface area S of a right cone is
S = πr2 + πrl
where r is the radius of the base and l is the slant height.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Specifying Units of Measure
Dec 15, 25 07:09 PM
Specifying Units of Measure -
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems