SUM OF THE ANGLES OF A TRIANGLE WORKSHEET

Problems 1-2 : Check whether the given angle measures can be the measures of a triangle.

Problem 1 :

45°, 75°, 60°

Problem 2 :

28°, 99°, 64°

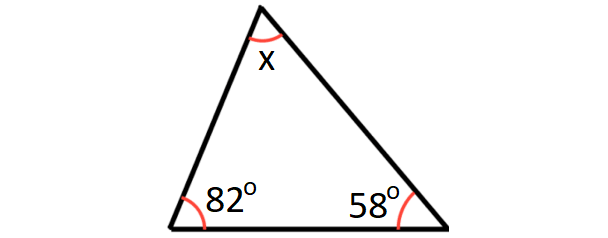
Problem 3 :

In the diagram shown below, what is the value of x?

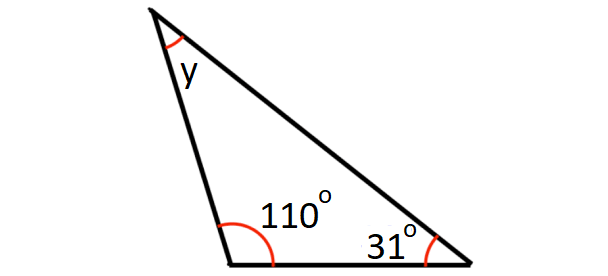
Problem 4 :

In the diagram shown below, what is the value of y?

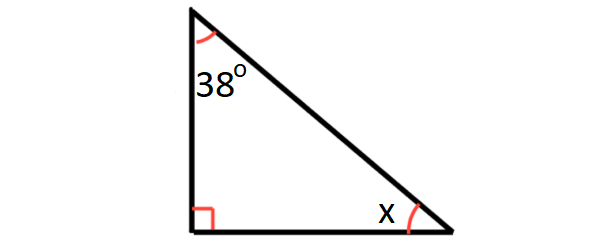
Problem 5 :

In the diagram shown below, what is the value of x?

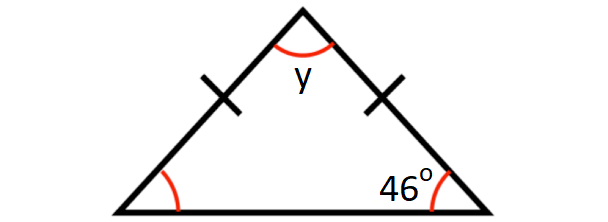
Problem 6 :

In the diagram shown below, what is the value of y?

Problem 7 :

In the diagram shown below, what is the value of a?

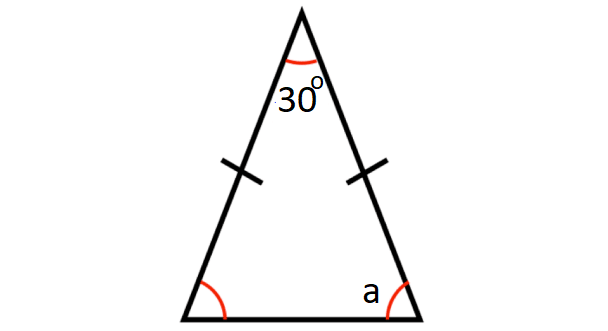
Problem 8 :

In the diagram shown below, what is the value of x?

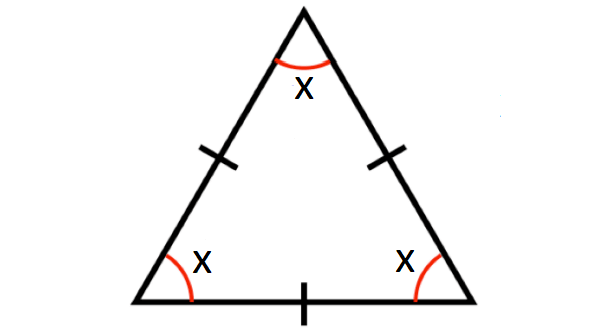
Problem 9 :

In the diagram shown below, what is the value of z?

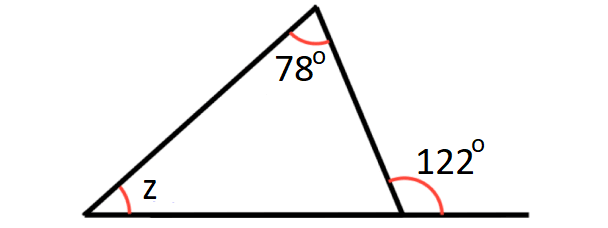
Problem 10 :

In the diagram shown below, what is the value of x?

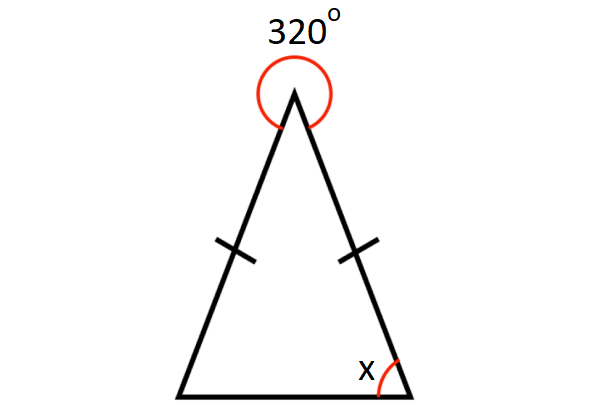
Problem 11 :

In the diagram shown below, what is the value of w?

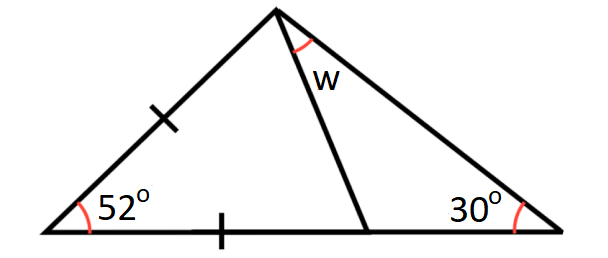
Problem 12 :

In the diagram shown below, what is the value of y?

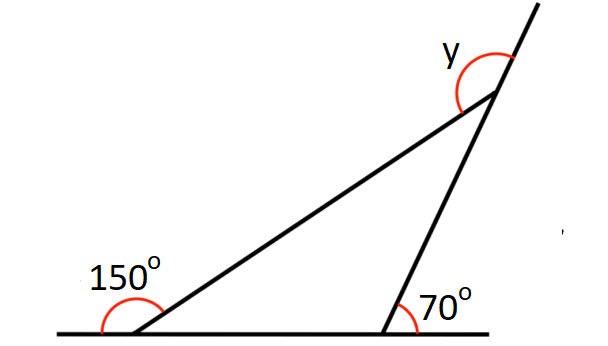
Problem 13 :

In the diagram shown below, what is the value of p?

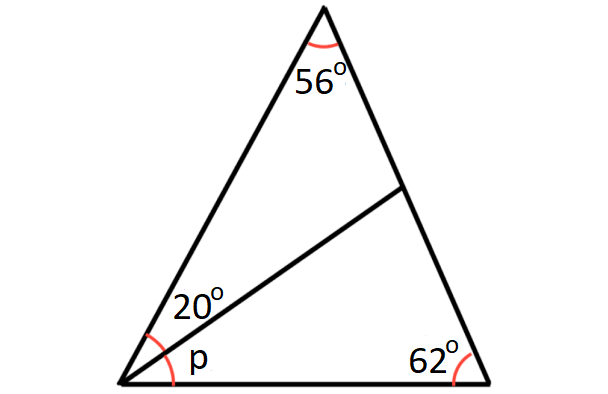
Problem 14 :

In the diagram shown below, what is the value of x?

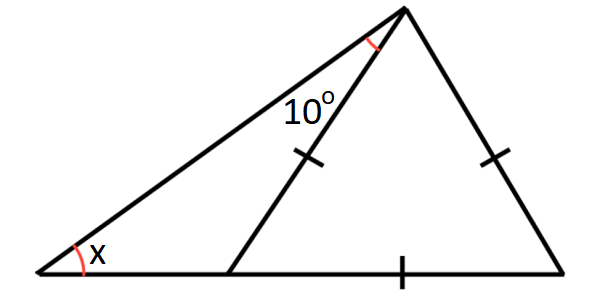
Problem 15 :

The first angle of a triangle is two-third of the third angle, the second angle is double the first angle. Find the three angles of the triangle.

Problem 16 :

In a triangle, sum of the first and second angles is 95°, sum of the second and third angles is 130° and sum of the first and third angles is 135°. Find the three angles of the triangle.

Problem 17 :

In the diagram shown below, triangle PQR is an isosceles triangle with PQ = PR and QRST is a rectangle.

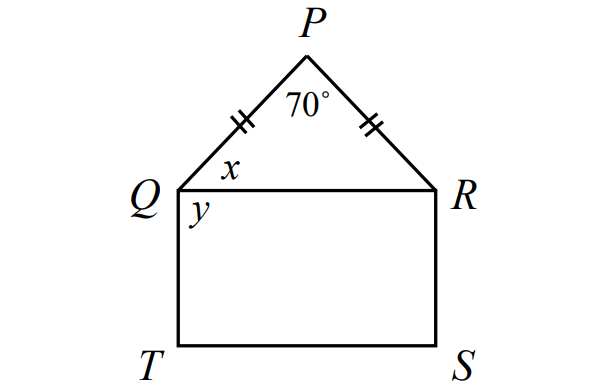
If m∠QPR = 70°, m∠PQR = x and m∠PQR = y, what is the value of (x + y)?

Problem 18 :

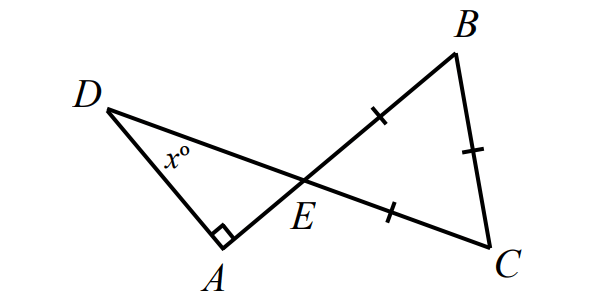
In the diagram shown below, AB and CD intersect at E. If triangle BCE is equilateral and triangle ADE is a right-angled triangle, what is the value of x?

Answers

1. Answer :

We know that the sum of the angles in a triangle is equal to 180°.

If the given angle measures add up to 180°, then they can be the angles of triangle.

45° +  75° + 60° = 180°

Since the given angles measures 45°, 75° and 60° add up to 180°, they can be the angles of a triangle.

2. Answer :

Add the given angle measures and chech if they all add up to 180°.

28° + 99° + 64° = 191° ≠ 180° 

Since the given angles measures 28°, 99° and 64° do not add up to 180°, they can not be the angles of a triangle.

3. Answer :

sum of the angles in a triangle = 180°

In the triangle shown above,

x + 82° + 58° = 180°

x + 140° = 180°

Subtract 140° from both sides.

x = 40°

4. Answer :

sum of the angles in a triangle = 180°

In the triangle shown above,

y + 110° + 31° = 180°

y + 141° = 180°

y = 39°

5. Answer :

sum of the angles in a triangle = 180°

In the triangle shown above,

x + 38° + 90° = 180°

x + 128° = 180°

x = 52°

6. Answer :

In a triangle, angles opposite to congruent sides must be congruent.

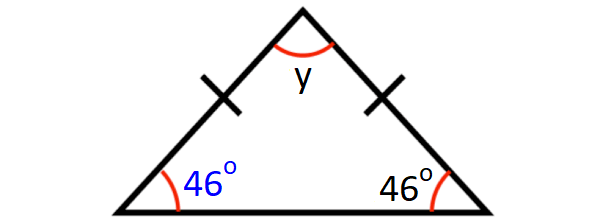
sum of the angles in a triangle = 180°

In the triangle shown above,

y + 46° + 46° = 180°

y + 92° = 180°

y = 88°

7. Answer :

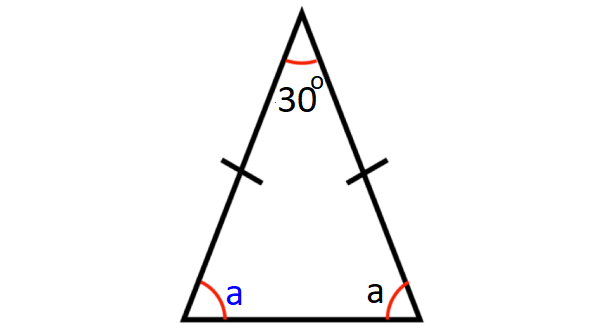
sum of the angles in a triangle = 180°

In the triangle shown above,

a + a + 30° = 180°

2a + 30° = 180°

2a = 150°

a = 75°

8. Answer :

sum of the angles in a triangle = 180°

In the triangle shown above,

x + x + x = 180°

3x = 180°

x = 60°

9. Answer :

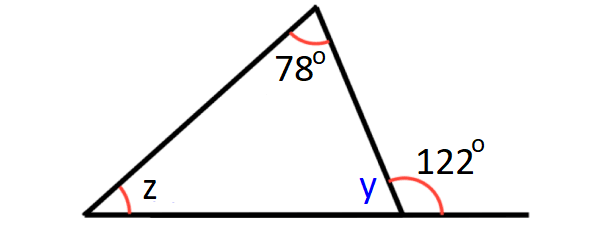
In the diagram shown above, y and 122° are linear pair.

y + 122° = 180°

y = 58°

sum of the angles in a triangle = 180°

y + z + 78° = 180°

Substitute y = 58°.

58° + z + 78° = 180°

z + 136° = 180°

z = 44°

10. Answer :

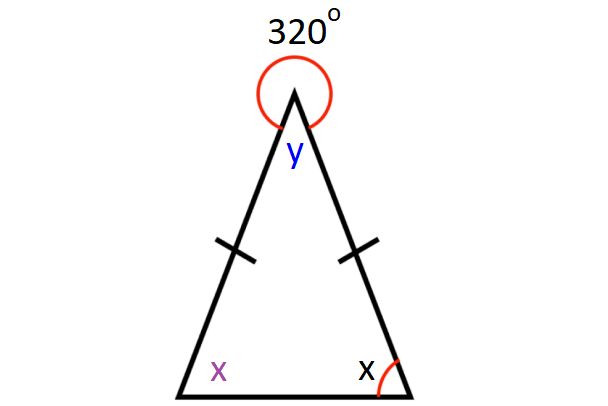
In the diagram shown above, y and 320° complete a full rotation.

y + 320° = 360°

y = 40°

sum of the angles in a triangle = 180°

x + x + y = 180°

2x + y = 180°

Substitute y = 40°.

2x + 40° = 180°

2x = 140°

x = 70°

11. Answer :

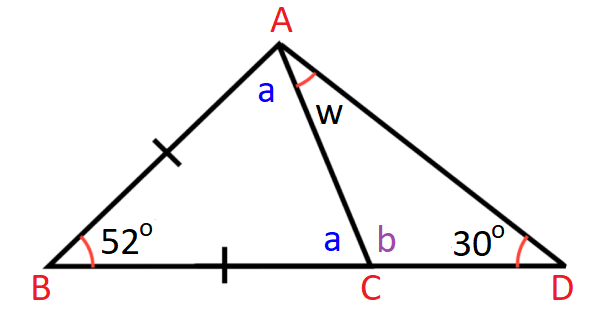
In ΔABC above,

a + a + 52° = 180°

2a + 52° = 180°

2a = 128°

a = 64°

In the diagram shown abpove, angles a and b are linear pair.

a + b = 180°

Substitute a = 64°

64° + b = 180°

b = 116°

In ΔACD above,

w + b + 30° = 180°

Substitute b = 116°.

w + 116° + 30° = 180°

w + 146° = 180°

w = 34°

12. Answer :

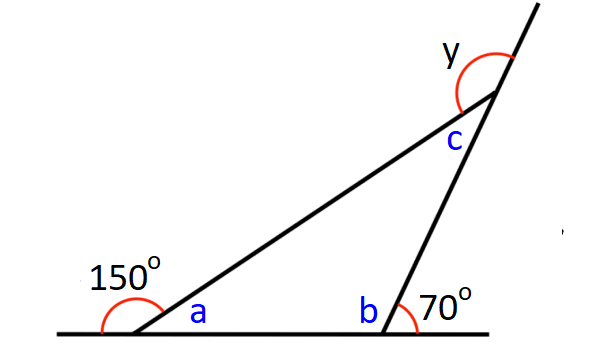
In the diagram shown above, a and 150° are linear pair.

a + 150° = 180°

a = 30°

b and 70° are linear pair.

b + 70° = 180°

b = 110°

In the triangle above,

a + b + c = 180°

Substitute a = 30° and b = 110°

30° + 110° + c = 180°

140° + c = 180°

c = 40°

c and y are linear pair.

c + y = 180°

Substitute c = 40°.

40° + y = 180°

y = 140°

13. Answer :

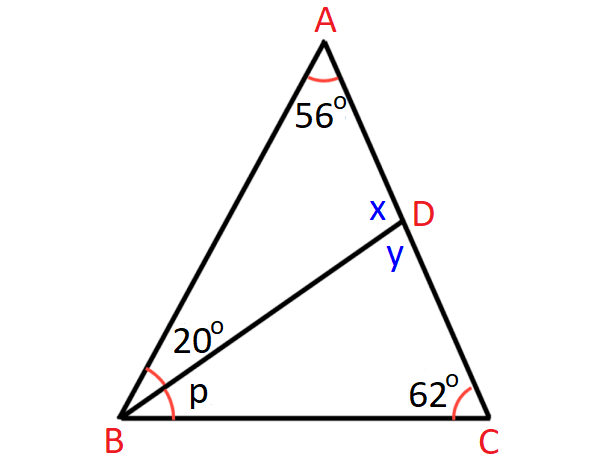
In ΔABD,

x + 56° + 20° = 180°

x + 76° = 180°

x = 104°

x and y are linear pair.

x + y = 180°

Substitute x = 104°.

104° + y = 180°

y = 76°

In ΔBCD,

p + y + 62° = 180°

Substitute y = 76°.

p + 76° + 62° = 180°

p + 138° = 180°

p = 42°

14. Answer :

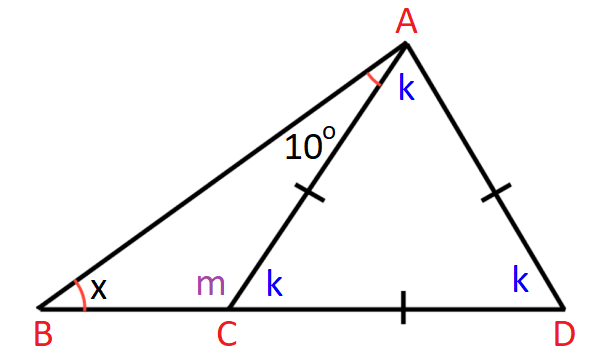
In ΔACD,

k + k + k = 180°

3k = 180°

k = 60°

k and m are linear pair.

k + m = 180°

Substitute k = 60°.

60° + m = 180°

m = 120°

In ΔABC,

x + m + 10° = 180°

Substitute m = 120°.

x + 120° + 10° = 180°

x + 130° = 180°

x = 50°

15. Answer :

Let x be the third angle.

Then, the first angle is ²ˣ⁄₃.

Second angle :

= 2 ⋅ ²ˣ⁄₃

= ⁴ˣ⁄₃

sum of the angles of a triangle = 180°

x + ²ˣ⁄₃ + ⁴ˣ⁄₃ = 180°

³ˣ⁄₃ + ²ˣ⁄₃ + ⁴ˣ⁄₃ = 180°

⁽³ˣ ⁺ ²ˣ ⁺ ⁴ˣ⁾⁄₃ = 180°

⁹ˣ⁄₃ = 180°

3x = 180°

x = 60°

third angle = 60°

first angle = ²ˣ⁄₃ = ²⁽⁶⁰⁾⁄₃ = 40°

second angle = ⁴ˣ⁄₃ = ⁴⁽⁶⁰⁾⁄₃ = 80°

The angles of the triangle are 40°, 80° and 60°.

16. Answer :

Let x, y and z be the first, second and third angles of the triangle respectively.

From the given information, we have

x + y = 95° -----(1)

y + z = 130° -----(2)

x + z = 135° -----(3)

Since x, y and z are the angles of a triangle,

x + y + z = 180°

Substitute 95° for 'x + y' [from (1)].

95° + z = 180°

z = 85°

Substitute z = 85° in (2).

y + 85° = 130°

y = 45°

Substitute y = 45° in (1).

x + 45° = 95°

x = 50°

The angles of the triangle are 50°, 45° and 85°.

17. Answer :

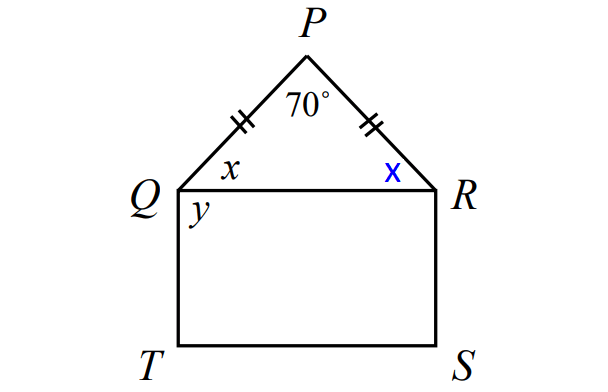
In ΔPQR above,

x + x + 70° = 180°

2x + 70° = 180°

2x = 110°

x = 55°

In a rectangle each vertex angle is a right angle.

y = m∠Q = 90°

x + y = 55° + 90°

= 145°

18. Answer :

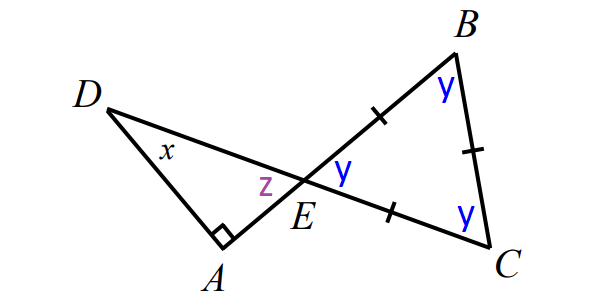
In ΔBCE above,

y + y + y = 180°

3y = 180°

y = 60°

In the diagram above, x and y are vertical angles

z = y

z = 60°

In triangle AED above,

x + z + 90° = 180°

Substitute z = 60°.

x + 60° + 90° = 180°

x + 150° = 180°

x = 30°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.