SQUARES AND SQUARE ROOTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If you multiply a number by itself, the result is a square number. This means that a square number is a number that is the product of two identical numbers. If n is a number, its square is represented by n2.
Square numbers can be represented visually as 2D squares. Square numbers are also called as perfect squares.
The perfect square of natural numbers are 1, 4, 9, 16, 25, 36, ... and so on.
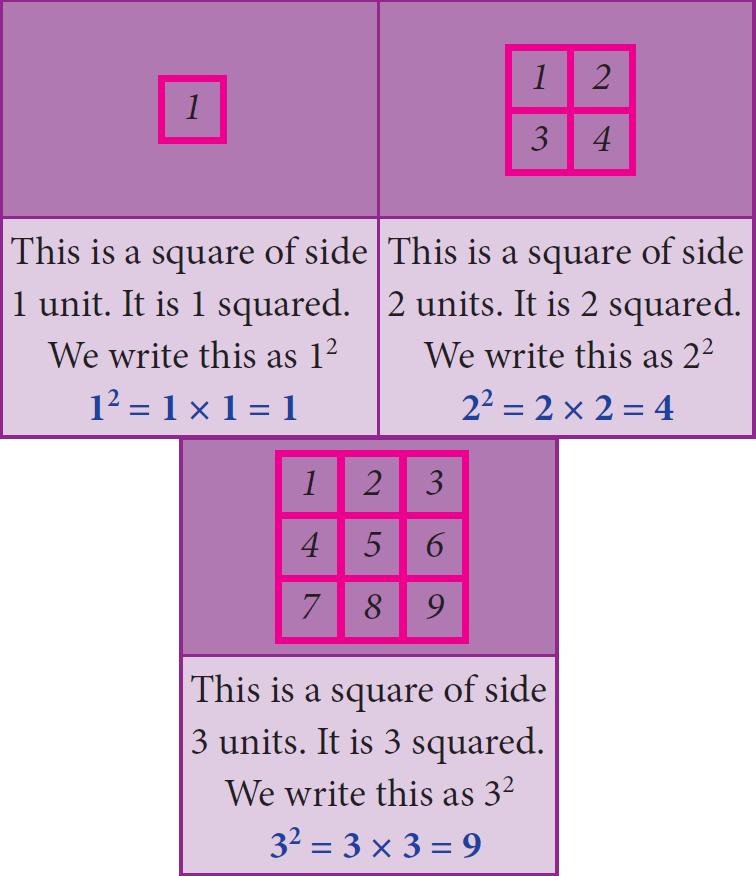
More often we write like this :
42 = 16
This says "4 squared is 16"
The 2 at the top stands for squared and it indicates the number of times the number 4 appears in the product
42 = 4 × 4 = 16
The numbers 1, 4, 9, 16, ... are all square numbers (also called perfect square numbers). Each of them is made up of the product of same two factors.
A natural number n is called a square number, if we can find another natural number m such that
n = m2
Is 49 a square number? Yes, because it can be written as 72. Is 50 a square number?
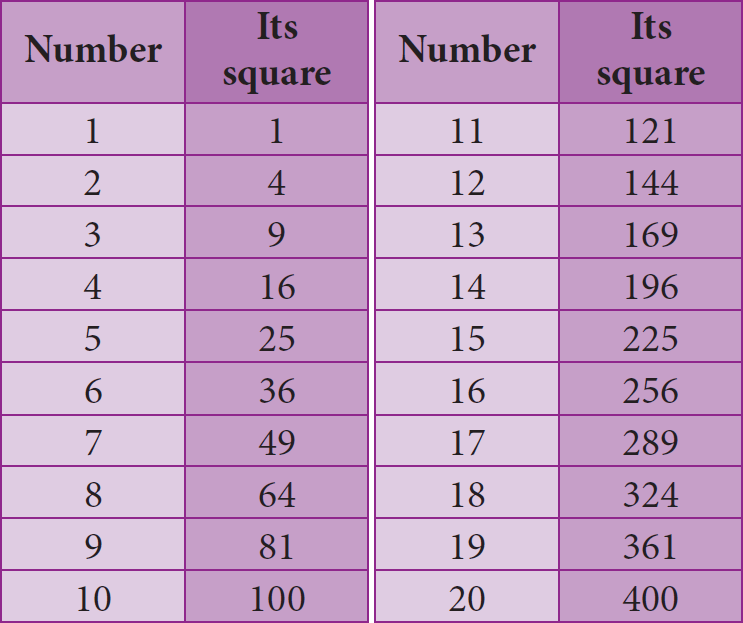
The following table gives the squares of numbers up to 20.
Properties of Square Numbers
• The square numbers end with 0, 1, 4, 5, 6 and 9 only.
• If a number ends with 1 or 9, its square ends with 1.
• If a number ends with 2 or 8, its square ends with 4.
• If a number ends with 3 or 7, its square ends with 9.
• If a number ends with 4 or 6, its square ends with 6.
• If a number ends with 5 or 0, its square also ends with 5 or 0 respectively.
• Square of an odd number is always odd and the square of an even number is always even.
• Numbers that end with 2,3,7 and 8 are not perfect squares.
• The square of a natural number other than 1, is either a multiple of 3 or exceeds a multiple of 3 by 1.
• The square of a natural number, other than 1, is either a multiple of 4 or exceeds a multiple of 4 by 1.
• The remainder of a perfect square when divided by 3, is either 0 or 1 but never 2.
• The remainder of a perfect square, when divided by 4, is either 0 or 1 but never 2 and 3.
• When a perfect square number is divided by 8, the remainder is either 0 or 1 or 4, but will never be equal to 2, 3, 5, 6 or 7.
Problem 1 :
The area of a square field is 3136 m2. Find its perimeter.
Solution :
Given that the area of the square field = 3136 m2
We can find square root of 3136 by long division.
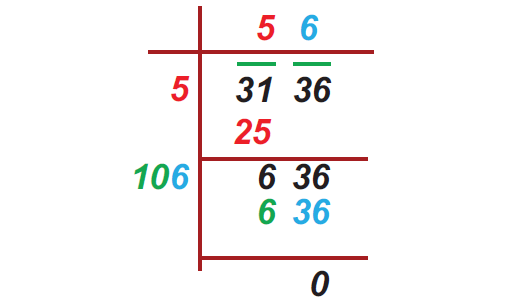
The side of square field :
= 56 m
The perimeter of the square field :
= 4 × side
= 4 × 56
= 224 m
Problem 2 :
A real estate owner had two plots, a square plot of side 39 m and a rectangular plot of dimensions 100 m length and 64 m width. He sells both of these plots and acquires a new square plot of the same area. What is the length of side of his new plot?
Solution :
The transactions can be visualised as follows :
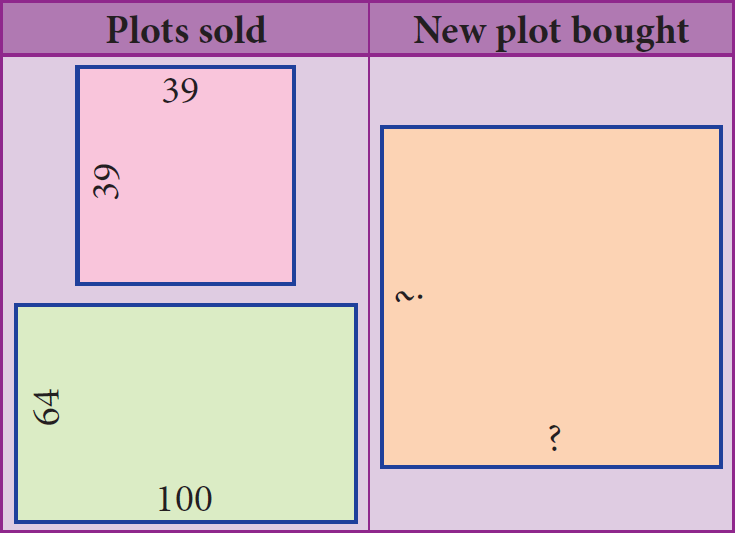
Area of the square plot bought
=
Area of the
square plot sold
+
Area of the
rectangular plot sold
= 39 × 39 + 100 × 64
= 1521 + 64000
= 7921 m2
We can find square root of 7921 by long division.
Length of a side of the new square plot :
= 89 m
Square Root
Squaring a number is another mathematical operation just like addition, subtraction, multiplication etc., Most mathematical operations have ‘inverse’ (meaning opposite’)
operations. For example, subtraction is the inverse of addition, division is the inverse of multiplication etc., Squaring also has an inverse operation namely finding the Square root.
The square root of a number n, written √n or n½, is the number that gives n when multiplied by itself. For example, √81 is 9, because 9 × 9 = 81.
In the table below, we have square roots of all the perfect squares starting from 1 to 100.

If 132 = 169, what is √169?
If 625 = 252, what is the square root of 625?
If we know that 361 = 192, we can immediately say that √361 is 19.
We have, 12 = 1 and so 1 is a square root of 1.
Similarly, (-1)2 = 1. So, (–1) is also a square root of 1.
We have, 22 = 4 and so 2 is a square root of 4.
Similarly, (-2)2 = 4. So, (–2) is also a square root of 4.
This continues as 32 = 9 and so 3 is a square root of 9. Similarly, (–3)2 = 9. So, (–3) is also a square root of 9.
So, when we find square root of a number, it will result the a number with positive and negative sign.
√9 = ±3
√9 = -3 or +3
The above examples suggest that there are two integral square roots for a perfect square number. However, in working out the problems, we will take up only positive integral square root. The positive square root of a number is always denoted by the symbol √.
Thus, √4 is 2 (and not –2). Also, √9 is 3 (and not –3). We have to remember that this is a universally accepted notation.
Square root through Prime Factoring
Study the following table giving the prime factors of numbers and those of their squares.
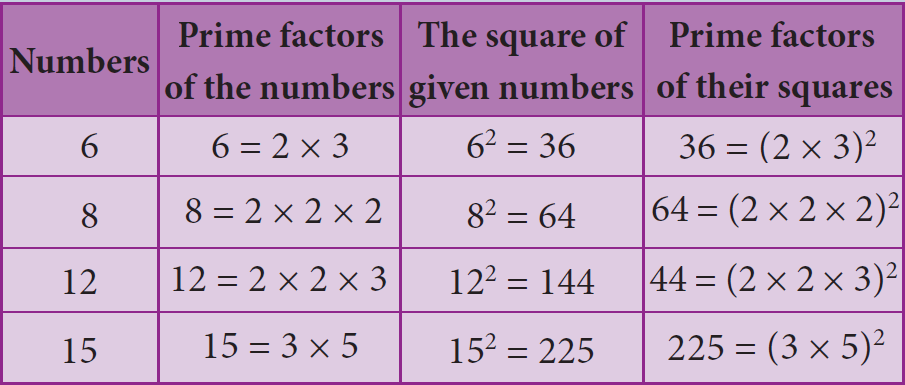
Look at 6 and its prime factors. How many times do 2 and 3 occur in 36 in the list? Now, look at its square 36 and its prime factors. How many times do 2 and 3 occur in 36 here?
Repeat the above task in the case of other numbers 8, 12, and 15 also. (We may also choose our own numbers and their squares). What do we find? We find that,
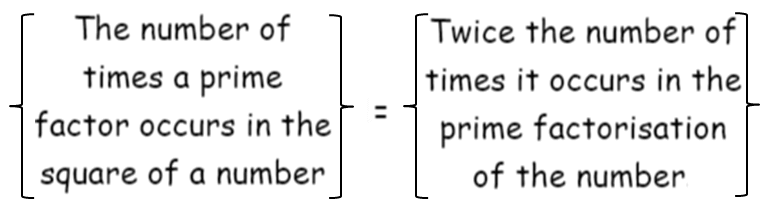
We use this idea to find the square root of a square number. First, resolve the given number into prime factors. Group the identical factors in pairs and then take one from them to find the square root.
Problem 3 :
Find the square root of 324 by prime factoring.
Solution :
First, resolve the given number into prime factors. Group the identical factors in pairs and then take one from them to find the square root.
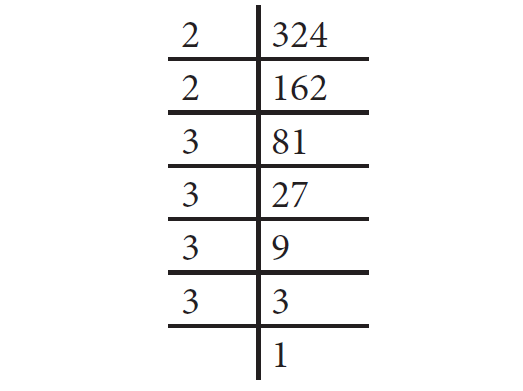
324 = 2 × 2 × 3 × 3 × 3 × 3
= 22 × 32 × 32
= (2 × 3 × 3)2
= 2 × 3 × 3
= 18
Problem 4 :
Find the least number by which 250 is to be multiplied (or) divided so that the resulting number is a perfect square. Also, find the square root in that case.
Solution :
First, resolve the given number into prime factors. Group the identical factors in pairs and then take one from them to find the square root.
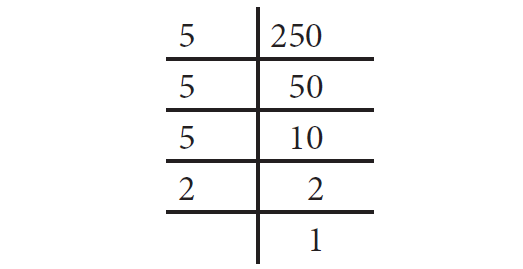
Here,
250 = 5 × 5 × 5 × 2
250 = 52 × 5 × 2
Here, the prime factors 5 and 2 do not have pairs.
Therefore, we can either divide 250 by 10 or multiply 250 by 10, because 10 is a least common multiple of 5 and 2.
If we multiply 250 by 10, we get
250 × 10 = 52 × 5 × 2 × 10
2500 = 52 × 5 × 2 × 5 × 2
Square root of 2500 :
= 5 × 5 × 2
= 50
If we divide 250 by 10, we get
25 = 52
Square root of 25 :
= 5
Problem 5 :
Is 108 a perfect square number?
Solution :
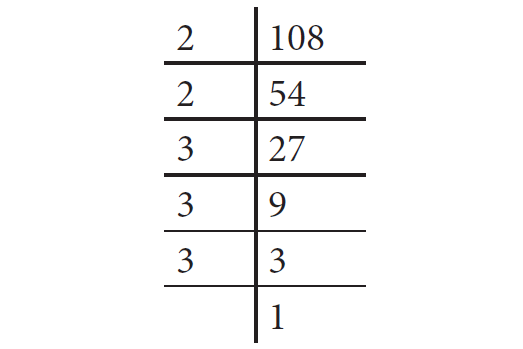
Here,
108 = 2 × 2 × 3 × 3 × 3
= 22 × 32 × 3
Here, the prime factor 3 does not have a second pair. Hence, 108 is not a perfect square number.
Finding The Square Root of a Number by Long Division Method
When we come across numbers with large number of digits, finding their square roots by factorisation becomes lengthy and diffi cult. Use of long division helps us in such cases. Let us look into the method with a couple of illustrations.
Illustration 1 :
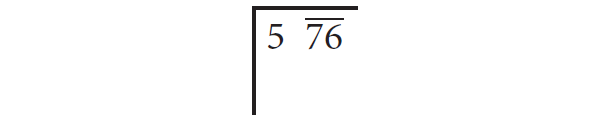
Find the square root of 576 by long division method.
Step 1 :
Group the digits in pairs, starting with the digit in the unit’s place. Each pair and the remaining digit (if any) is called a period. Put a bar over every pair of digits starting from the right of the given number. If there are odd number of digits, the extreme left digit will be without a bar sign above it.
Step 2 :
Th ink of the largest number whose square is equal to or just less than the fi rst period. Take this number as the divisor and also as the quotient. The left extreme number here is 5. Th e largest number whose square is less than or equal to 5 is 2. Th is is our divisor and the quotient.
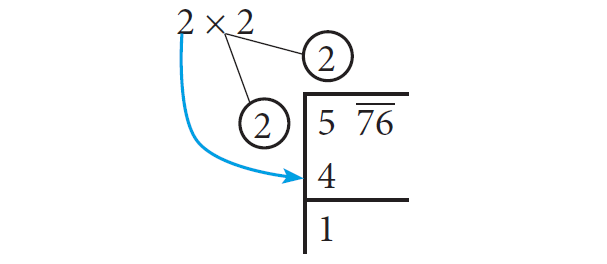
Step 3 :
Bring 76 down and write it down to the right of the remainder 1. Now, the new dividend is 176.
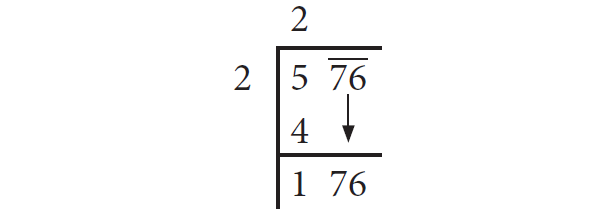
Step 4 :
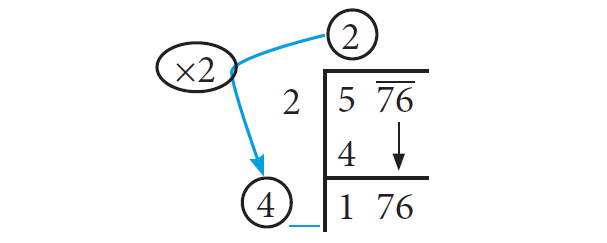
To find the new divisor, multiply the earlier quotient (2) by 2 (always) and write it leaving a blank space next to it.
Step 5 :
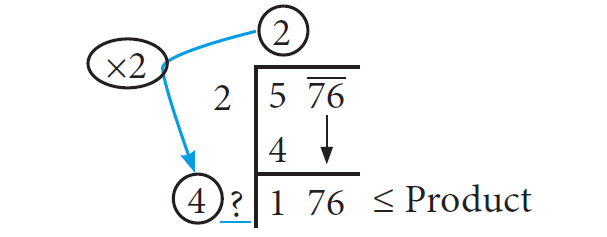
The new divisor is 4 followed by a digit. We should choose this digit next to 4 such that the new quotient multiplied by the new divisor will be less than or equal to 176.
Step 6 :
Clearly, the required digit here has to be 4 or 6. (Why?) When we calculate, 46 x 6 = 276 whereas 44 x 4 = 176. So, we put 4 in the blank space and write 44 x 4 = 176 below 176 and subtract to get the remainder 0 and the quotient at the top, that is 24 is the square root of 576.
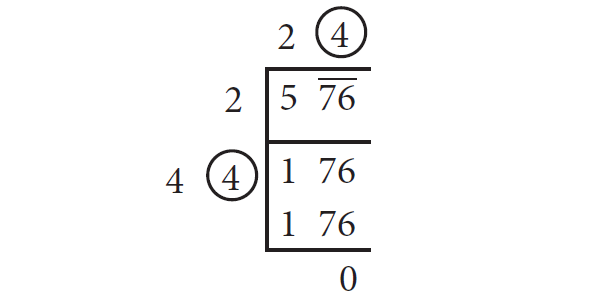
Therefore,
√576 = 24
Illustration 2 :
In the following example, follow the figures one after another and try to understand what each figure explains, the stage by stage and the gradual computation of computing the square root of 288369.
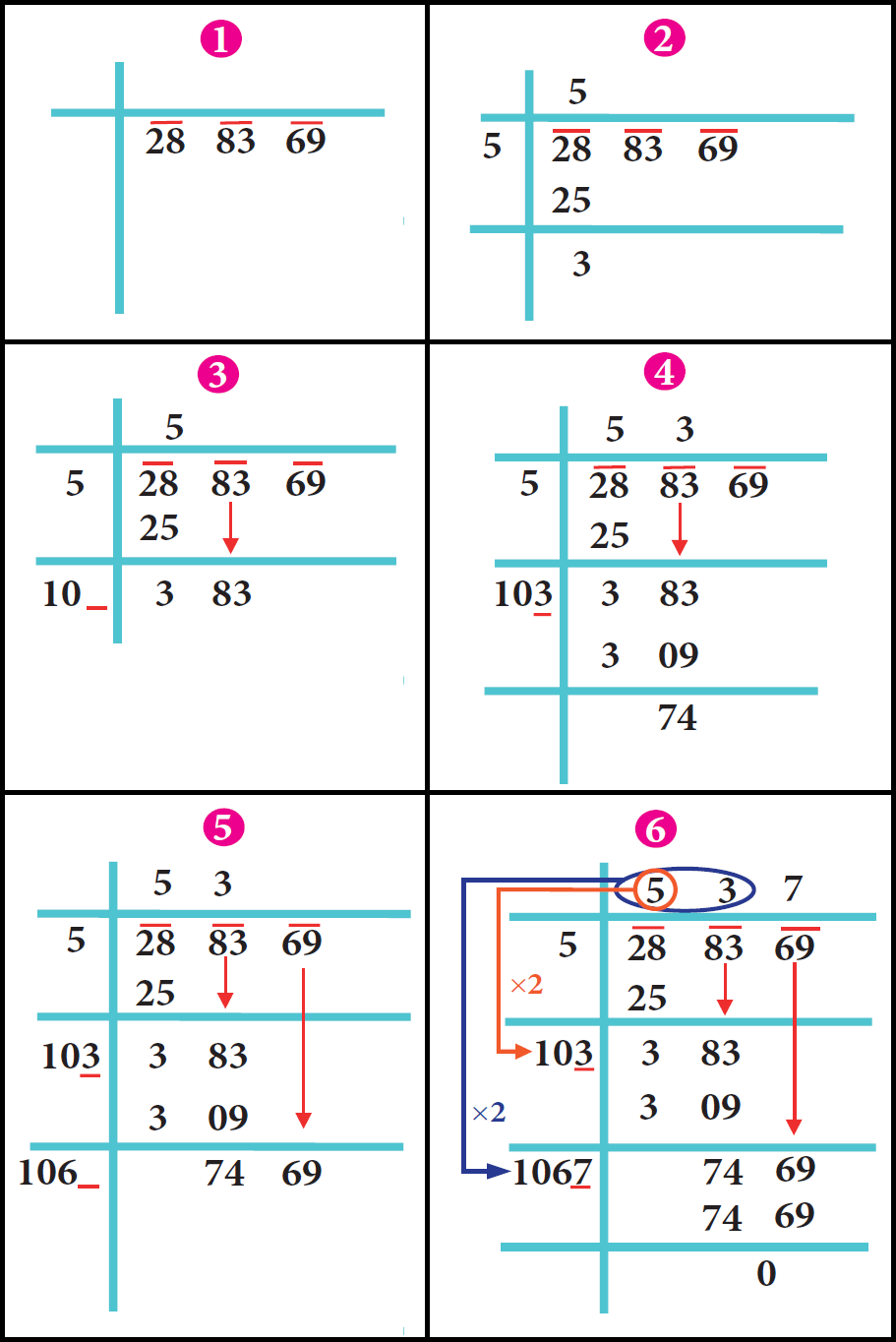
We find that
Problem 6 :
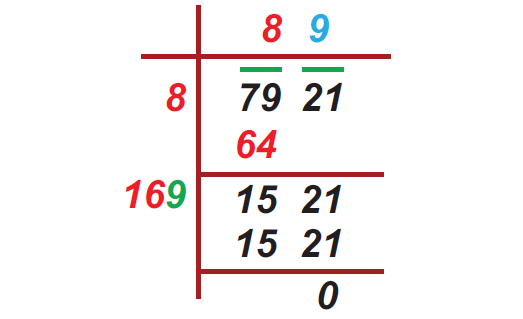
Find the square root of 459684 by long division method.
Solution :
By long division method, we can find the square root of 459684 as given below :
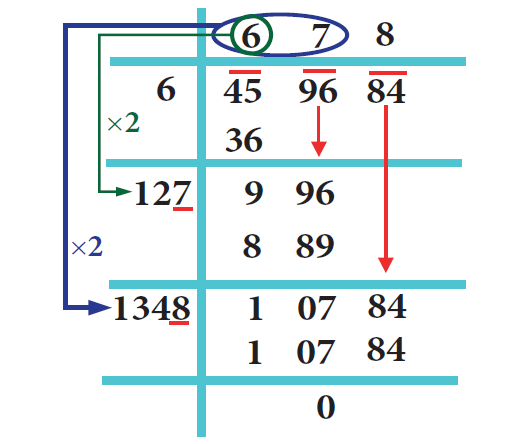
Therefore,
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
