SQUARES AND SQUARE ROOTS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
In what digits will square numbers end with?
Problem 2 :
If a number ends with the digit 1 or 9, in what digit will its square ends with?
Problem 3 :
If a number ends with the digit 2 or 8, in what digit will its square ends with?
Problem 4 :
If a number ends with the digit 3 or 7, in what digit will its square ends with?
Problem 5 :
If a number ends with the digit 4 or 6, in what digit will its square ends with?
Problem 6 :
If a number ends with the digit 0 or 5, in what digit will its square ends with?
Problem 7 :
What is the square of an odd number?
Problem 8 :
What is the square of an even number?
Problem 9 :
How to identify a number, which is not a perfect square?
Problem 10 :
If a natural number other than 1 is squared, what is the result?
Problem 11 :
What is the remainder of a perfect square, when divided by 3?
Problem 12 :
What is the remainder of a perfect square, when divided by 4?
Problem 13 :
What is the remainder of a perfect square, when divided by 8?
Problem 14 :
If the area of a square field is 3136 ft2. what is its perimeter.
Problem 15 :
There are two plots, in which, a square plot of side 39 yards and a rectangular plot of dimensions 100 yards length and 64 yards width. Both the plots are sold and acquired a new square plot of the same area. Find the length of side of the new plot.
Problem 16 :
What is square root?
Problem 17 :
Is the square of a number positive or negative?
Problem 18 :
Find the square root of 324 by prime factoring.
Problem 19 :
What is the smallest number by which 250 has to be multiplied (or) divided so that the resulting number is a perfect square? Also, find the square root in that case.
Problem 20 :
Check, if 108 is a perfect square.
Problem 21 :
If x2 = 459684 and x > 0, find the value of x.

Answers
1. Answer :
The square numbers will end with the digits 0, 1, 4, 5, 6 and 9 only.
Examples :
102 = 10 × 10 = 100
112 = 11 × 11 = 121
122 = 12 × 12 = 144
52 = 5 × 5 = 25
62 = 6 × 6 = 36
132 = 13 × 13 = 169
2. Answer :
If a number ends with the digit 1 or 9, its square will end with the digit 1.
Examples :
112 = 11 × 11 = 121
92 = 9 × 9 = 81
3. Answer :
If a number ends with the digit 2 or 8, its square will end with the digit 4.
Examples :
122 = 12 × 12 = 144
142 = 14 × 14 = 196
4. Answer :
If a number ends with the digit 3 or 7, its square will end with the digit 9.
Examples :
132 = 13 × 13 = 169
172 = 17 × 17 = 289
5. Answer :
If a number ends with the digit 4 or 6, its square will end with the digit 6.
Examples :
142 = 14 × 14 = 196
162 = 16 × 16 = 256
6. Answer :
If a number ends with the digit 0 or 5, its square also will end with the digit 0 or 5 resepctively.
Examples :
102 = 10 × 10 = 100
152 = 15 × 15 = 225
7. Answer :
Square of an odd number is always odd.
Examples :
72 = 7 × 7 = 49
192 = 19 × 19 = 361
8. Answer :
Square of an even number is always even.
Examples :
42 = 4 × 4 = 16
122 = 12 × 12 = 144
9. Answer :
Numbers that end with 2,3,7 and 8 are not perfect squares.
Examples :
13, 32, 47
10. Answer :
If the square of a natural number other than 1 is squared, the result is either a multiple of 3 or exceeds a multiple of 3 by 1 or a multiple of 4 or exceeds a multiple of 4 by 1.
Examples :
22 = 2 × 2 = 4 (multiple of 4)
22 = 2 × 2 = 4 (exceeds a multiple of 3 by 1)
32 = 3 × 3 = 9 (multiple of 3)
52 = 5 × 5 = 25 (exceeds a multiple of 4 by 1)
11. Answer :
The remainder of a perfect square when divided by 3, is either 0 or 1 but never 2.
12. Answer :
The remainder of a perfect square, when divided by 4, is either 0 or 1 but never 2 and 3.
13. Answer :
When a perfect square number is divided by 8, the remainder is either 0 or 1 or 4, but will never be equal to 2, 3, 5, 6 or 7.
14. Answer :
Given : Area the square field = 3136 ft2
Find the square root of 3136 by long division.
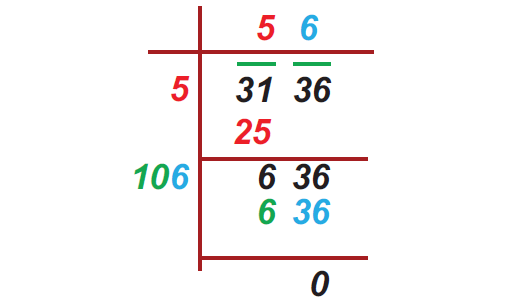
The side of square field :
= 56 ft.
The perimeter of the square field :
= 4 × side
= 4 × 56
= 224 ft.
15. Answer :
The transactions can be visualised as follows :
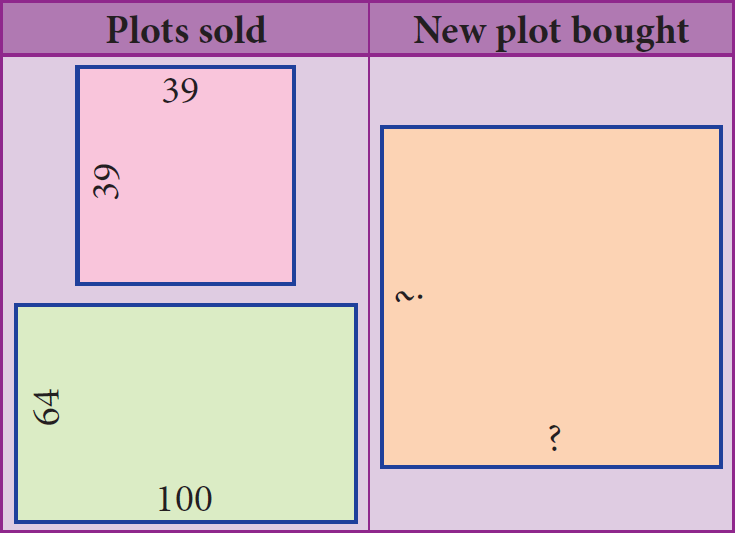
Area of the square plot bought
=
Area of the
square plot sold
+
Area of the
rectangular plot sold
= 39 × 39 + 100 × 64
= 1521 + 64000
= 7921 yd2
Find the square root of 7921 by long division.
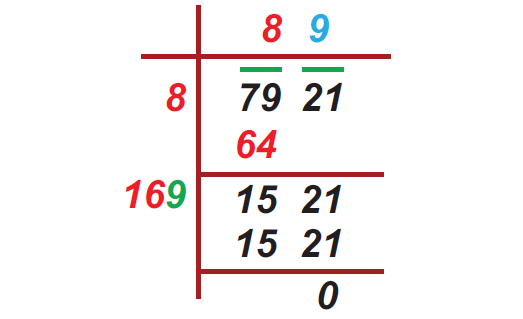
Length of a side of the new square plot :
= 89 yd.
16. Answer :
Most mathematical operations have ‘inverse’ (meaning ‘opposite’) operations. For example, subtraction is the inverse of addition, division is the inverse of multiplication etc., Squaring also has an inverse operation namely finding the Square root.
If you square 5, it results 25. If you find square root of 25, it will result 5.
52 = 25
√25 = 5
17. Answer :
The square root of a number is either positive or negative.
For example, 52 = 25. So, 5 is a square root of 25. Similarly, (–5)2 = 25. So, (–5) is also a square root of 25.
√25 = ±5
√25 = -5 or +5
18. Answer :
Step 1 :
Write 324 as the product of its prime factors
Step 2 :
Group the identical factors in pairs.
Step 3 :
Take one prime factor out for every two identical prime factors multiplied inside the square root.
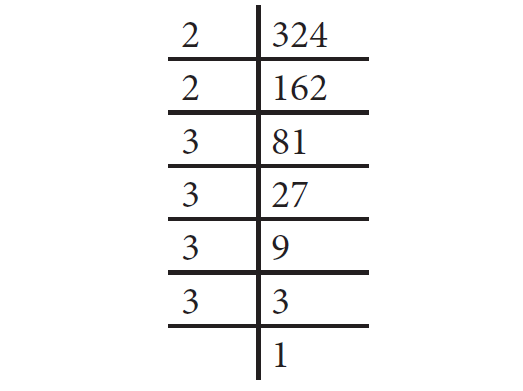
324 = 2 × 2 × 3 × 3 × 3 × 3
= 22 × 32 × 32
= (2 × 3 × 3)2
= 2 × 3 × 3
= 18
19. Answer :
Write 250 as the product of its prime factors
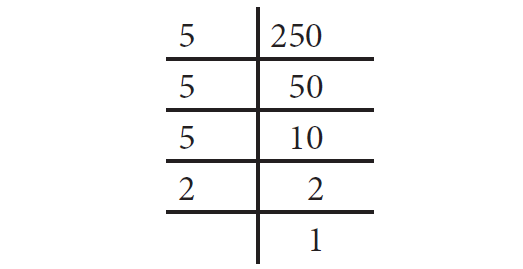
Here,
250 = 5 × 5 × 5 × 2
250 = 52 × 5 × 2
Here, the prime factors 5 and 2 do not have pairs.
10 is a least common multiple of 5 and 2.
So, 250 can either be divided by 10 or multiplied 10,
If 250 is multiplied by 10,
250 × 10 = 52 × 5 × 2 × 10
2500 = 52 × 5 × 2 × 5 × 2
Square root of 2500 :
= 5 × 5 × 2
= 50
If 250 is divided by 10,
25 = 52
Square root of 25 :
= 5
20. Answer :
Write 108 as the product of its prime factors
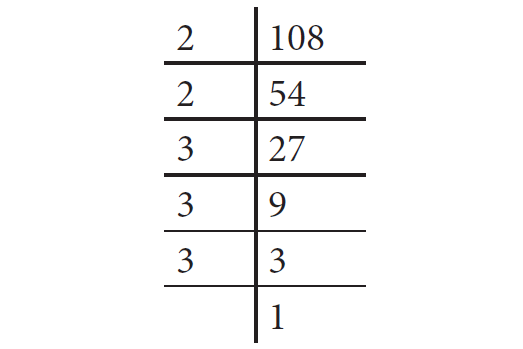
Here,
108 = 2 × 2 × 3 × 3 × 3
= 22 × 32 × 3
Here, the prime factor 3 does not have a second pair.
So, 108 is not a perfect square number.
21. Answer :
x2 = 459684
The square root of 459684 can be found by long division as shown below.
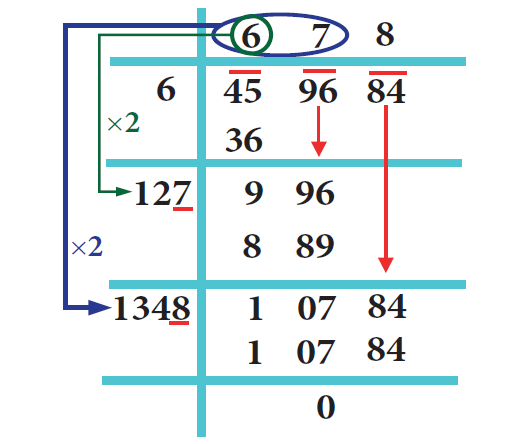
x = ± 678
Since x > 0,
x = 678
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

