SQUARE ROOT OF A NUMBER WORKSHEET

Problems 1-9 : In each case, evaluate the square root by prime factorisation :

Problem 1 :

√4

Problem 2 :

√49

Problem 3 :

√18

Problem 4 :

√81

Problem 5 :

√92

Problem 6 :

√0.25

Problem 7 :

√2.25

Problem 8 :

√0.09

Problem 9 :

√0.0001

Problems 10-11 : Evaluate the square root using long division :

Problem 10 :

√288369

Problem 11 :

√459684

Problems 12-20 : Solve for x.

Problem 12 :

x² = 4

Problem 13 :

x² - 5 = -5

Problem 14 :

4x² = 256

Problem 15 :

25x² = 4

Problem 16 :

x² + 1.8 = 2.29

Problem 17 :

(7x² + 3)/2 = 15.5

Problem 18 :

1 - 2x² = -287

Problem 19 :

(x + 5)² = 4

Problem 20 :

3(3x - 2)² = 147

Answers

1. Answer :

√4 = √(2 ⋅ 2)

= 2

2. Answer :

√49 = √(7 ⋅ 7)

= 7

3. Answer :

√18 = √(2 ⋅ 3 ⋅ 3)

= 3√2

4. Answer :

√81 = √(3 ⋅ 3 ⋅ 3 ⋅ 3)

= 3 ⋅ 3

= 9

5. Answer :

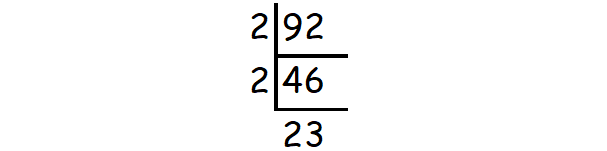
√92 = √(2 ⋅ 2 ⋅ 23)

= 2√23

6. Answer :

√0.25

Inside the square root, there is a decimal number. To get rid of the decimal point, 0.25 can be written as a fraction. In 0.25, since there are two digits after the decimal point, it can be written as a fraction with denominator 100.

√0.25 = √²⁵⁄₁₀₀

= √(⁵⁄₁₀ ⋅ ⁵⁄₁₀) 

= ⁵⁄₁₀

= 0.5

7. Answer :

√2.25 = √²²⁵⁄₁₀₀

= √(¹⁵⁄₁₀ ⋅ ¹⁵⁄₁₀) 

= ¹⁵⁄₁₀

= 1.5

8. Answer :

√0.09 = √⁹⁄₁₀₀

= √(³⁄₁₀ ⋅ ³⁄₁₀) 

= ³⁄₁₀

= 0.3

9. Answer :

√0.0001 = √¹⁄₁₀₀₀₀

= √(¹⁄₁₀₀ ⋅ ¹⁄₁₀₀) 

= ¹⁄₁₀₀

= 0.01

10. Answer :

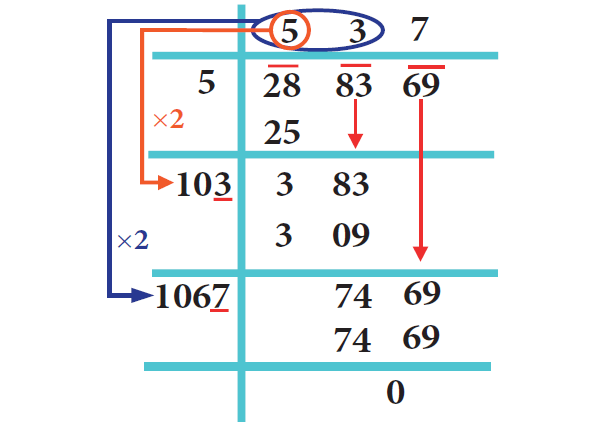
√288369 = 537

Click here to get step by step guide on finding square root of a number by long division method.

11. Answer :

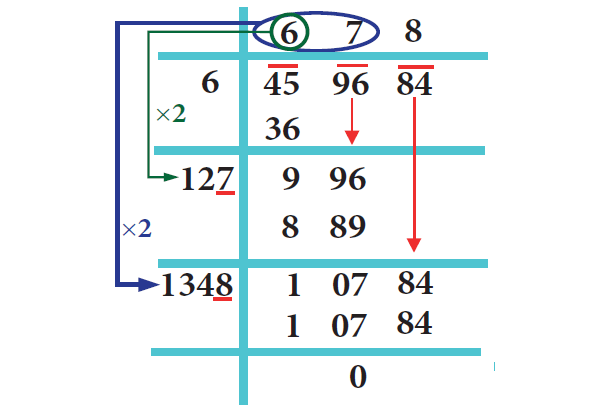
√459684 = 678

12. Answer :

To get rid of the square on the left side, take square root on both sides.

√x² = ±√4

x = ±√(2 ⋅ 2) 

x = ±2

x = -2  or  x = 2

13. Answer :

x² - 5 = -5

Add 5 to both sides.

x² = 0

Take square root on both sides.

√x² = ±√0

x = 0

14. Answer :

4x² = 256

Divide both sides by 4.

x² = 64

Take square root on both sides.

√x² = ±√64

x = ±√(8 ⋅ 8)

x = ±8

x = -8  or  y = 8

15. Answer :

25x² = 4

Divide both sides by 36.

x² = ⁴⁄₂₅

Take square root on both sides.

√x² = ±√⁴⁄₂₅

x = ±√(⅖ ⋅ ⅖)

x = ±⅖

x = -⅖  or  x = ⅖

16. Answer :

x² + 1.8 = 2.29

Subtract 1.8 from both sides.

x² = 0.49

x² = ⁴⁹⁄₁₀₀

Take square root on both sides.

√x² = ±√⁴⁹⁄₁₀₀

x = ±√(⁷⁄₁₀ ⋅ ⁷⁄₁₀)

x = ±⁷⁄₁₀

x = -⁷⁄₁₀  or  x = ⁷⁄₁₀

17. Answer :

(7x² + 3)/2 = 15.5

Multiply both sides by 2.

7x² + 3 = 31

Subtract 3 from both sides.

7x² = 28

Divide both sides by 7.

x² = 4

Take square root on both sides.

√x² = ±√4

x = ±√(2 ⋅ 2)

x = ±2

x = -2  or  x = 2

18. Answer :

1 - 2x² = -287

Subtract 1 from both sides.

-2x² = -288

Divide both sides by -2.

x² = 144

Take square root on both sides.

√x² = ±√144

x = ±√(12 ⋅ 12)

x = ±12

x = -12  or  x = 12

19. Answer :

(x + 5)² = 4

Take square root on both sides.

√(x + 5)² = ±√4

x + 5 = ±2

20. Answer :

3(3x - 2)² = 147

Divide both sides by 3.

(3x - 2)² = 49

Take square root on both sides.

√(3x - 2)² = ±√49

3x - 2 = ±7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.