HOW TO SOLVE A SYSTEM OF LINEAR EQUATIONS BY SUBSTITUTION

Examples 1-5 : Solve the given system of linear equations by substitution.

Example 1 :

x - 5y + 17 = 0

 2x + y + 1 = 0

Solution :

The above explained steps have been illustrated for the given system of linear equations in the picture shown below.

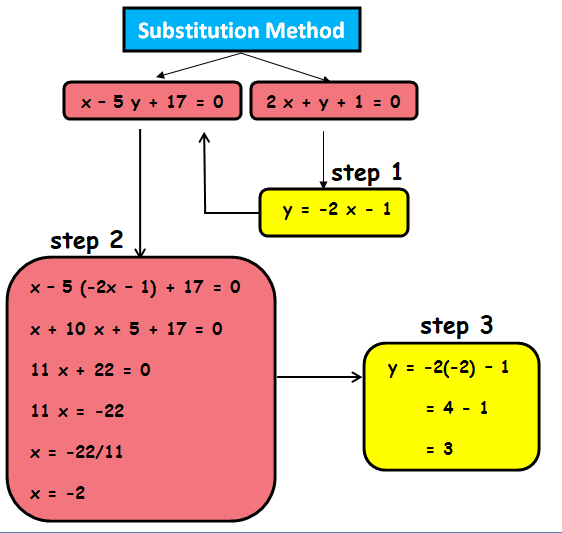
The solution is (-2, 3).

Example 2 :

5x - 3y - 8 = 0

2x - 3y - 5 = 0

Solution :

5x - 3y - 8 = 0 ----(1)

2x - 3y - 5 = 0 ----(2)

We find 3y in both equations.

Solve (1) for 3y.

5x - 3y - 8 = 0

Add 3y to both sides.

5x - 8 = 3y

or

3y = 5x - 8 ----(3)

Substitute 3y = 5x - 8 into (2).

2x - (5x - 8) - 5 = 0

2x - 5x + 8 - 5 = 0

-3x + 3 = 0

Subtract 3 from both sides.

-3x = -3

Divide both sides by -3.

x = 1

Substitute x = 1 into (3).

3y = 5(1) - 8

3y = 8 - 8

3y = -3

Divide both sides by 3.

y = -1

The solution is (1, -1).

Example 3 :

y = 6x - 11

-2x - 3y = -7

Solution :

y = 6x - 11 ----(1)

-2x - 3y = -7 ----(2)

In the given two equations, already (1) is solved for y. 

Substitute y = 6x - 11 into (2). 

-2x - 3(6x - 11) = -7

-2x - 18x + 33 = -7

-20x + 33 = -7

Subtract 33 from both sides. 

-20x = -40

Divide both sides by -20.

x = 2

Substitute x = 2 into (1).

y = 6(2) - 11

y = 12 - 11

y = 1

Thew solution is (2, 1).

Example 4 :

2x - 3y = -1

y = x - 1

Solution :

2x - 3y = -1 ----(1)

y = x - 1 ----(2)

In the given two equations, already (2) is solved for y. 

Substitute y = x - 1 into (1).

2x - 3(x - 1) = -1

2x - 3x + 3 = -1

-x + 3 = -1

Subtract 3 from both sides.

-x = -4

Multiply both sides by -1.

x = 4

Substitute x = 4 into (2).

y = 4 - 1

y = 3

The solution is (4, 3).

Example 5 :

y = -3x + 5

5x - 4y = -3

Solution :

y = -3x + 5 ----(1)

5x - 4y = -3 ----(2)

In the given two equations, already (1) is solved for y.

Substitute y = -3x + 5 into (2).

5x - 4(-3x + 5) = -3

5x + 12x - 20 = -3

17x - 20 = -3

Add 20 to both sides.

17x = 17

Divide both sides by 17.

x = 1

Substitute x = 1 into (1).

y = -3(1) + 5

y = -3 + 5

y = 2

The solution is (1, 2).

Example 6 :

The sum of two numbers is equal to 15. If the first number is equal to 5 less than three times the second number, find the numbers.

Solution :

Let x be the first number and y be the second number.

From the given information,

x + y = 15 ----(1)

x = 3y - 5 ----(2)

Substitute x = 3y - 5 into (1).

(3y - 5) + y = 15

3y - 5 + y = 15

4y - 5 = 15

Add 5 to both sides.

4y = 20

Divide both sides by 4.

y = 5

Substitute y = 5 into (2).

x = 3(5) - 5

x = 15 - 5

x = 10

The numbers are 10 and 5.

Example 7 :

Two angles are complementary. If one of the angles is equal to 15° more than twice the other angle, find the angles measures.

Solution :

Let x and y be the required angle measures.

Since the angles are complementary, they must add upto 90°.

x + y = 90° ----(1)

It is given that one of the angles is equal to 15° more than twice the other angle.

x = 2y + 15° ----(2)

Substitute x = 2y + 15° into (1).

2y + 15° + y = 90°

3y + 15° = 90°

Subtract 15° from both sides.

3y = 75°

Divide both sides by 3.

y = 25°

Substitute y = 25° into (2).

x = 2(25°) + 15°

x = 50° + 15°

x = 65°

The angle measures are 65° and 25°.

Example 8 :

The sum of the ages father and son is 55 years. The age of the father is 10 years more than two times the age of the son. Find the ages of the father and son.

Solution :

Let f be the age of the father and s be the age of the son.

From the given information,

f + s = 55 ----(1)

f= 2s + 10 ----(2)

Substitute f = 2s + 10 into (1).

2s + 10 + s = 55

3s + 10 = 55

Subtract 10 from both sides.

3s = 45

Divide both sides by 3.

s = 15

Substitute s = 15 into (2).

f = 2(15) + 10

f = 30 + 10

f = 40

The age of the father is 40 years and that of the son is 15 years.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.