SOLVING RIGHT TRIANGLES

Every right triangle has one right angle, two acute angles, one hypotenuse, and two legs.

To solve a right triangle means to determine the measures of all six parts. We can solve a right triangle if we know either of the following :

(i)  Two side lengths.

(ii)  One side length and one acute angle measure.

We can use the side lengths of a right triangle to find trigonometric ratios for the acute angles of the triangle.

In this section, we will learn how to find the measure of the angle using calculator, if we know the trigonometric ratios : the sine, the cosine or the tangent of an acute angle.  

In general, for an acute angle A :

If sin A  =  x, then ∠A  =  sin^-1x

If cos A  =  x, then ∠A  =  cos^-1x

If tan A  =  x, then ∠A  =  tan^-1x

Finding Angles in Right Triangles - Activity

Step 1 :

Carefully draw right ΔABC with side lengths of 3 centimeters, 4 centimeters, and 5 centimeters, as shown below.

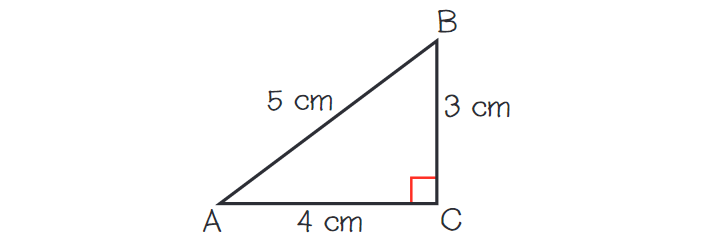
Step 2 : 

Use trigonometric ratios to find the sine, the cosine, and the tangent of ∠A. Express the ratios in decimal form.

Step 3 : 

In step 2, we found that sin A = 3/5 = 0.6. We can use calculator to find sin^-1(0.6). Most calculators use one of the keystroke sequences below.

Make sure your calculator is in degree mode. Then use each of the trigonometric ratios you found in Step 2 to approximate the measure of ∠A to the nearest tenth of a degree.

Step 4 :

Use a protractor to measure ∠A. How does the measured value compare with your calculated values?

Solving a Right Triangle

Example 1 :

Solve the right triangle shown below and round decimals to the nearest tenth.

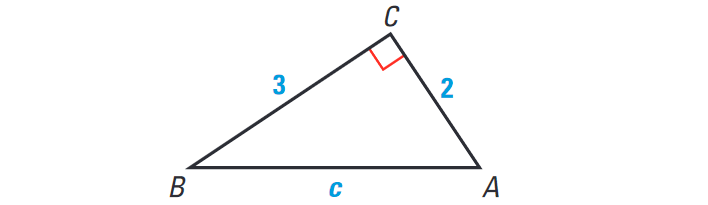
Solution :

Begin by using the Pythagorean Theorem to find the length of the hypotenuse.

Pythagorean Theorem : 

(Hypotenuse)²  =  (Leg)² + (Leg)²

Substitute.

c²  =  2² + 3²

Simplify.

c²  =  4 + 9

c²  =  13

Take square root on each side. 

√c²  =  √13

c  =  √13

Use calculator to approximate.

c  ≈  3.6

Now, use a calculator to find the measure of ∠B :

Finally, because ∠A and ∠B are complements, we can write

m∠A  =  90° - ∠B  ≈  90° - 33.7°  =  56.3°

The side lengths of the triangle are 2, 3, and √13, or about 3.6. The triangle has one right angle and two acute angles whose measures are about 33.7° and 56.3°.

Example 2 :

Solve the right triangle shown below and round decimals to the nearest tenth.

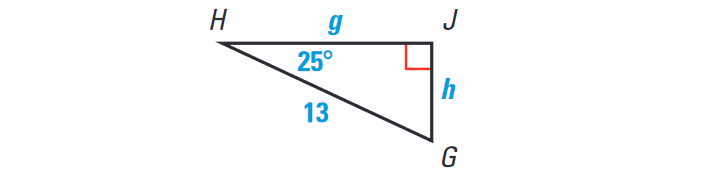
Solution :

Use trigonometric ratios to find the values of g and h.

Because ∠H and ∠G are complements, we can write

m∠G  =  90° - ∠H  =  90° - 25°  =  65°

The side lengths of the triangle are about 5.5, 11.8, and 13. The triangle has one right angle and two acute angles whose measures are 65° and 25°.

Using Right Triangles in Real Life

Example 3 :

During a space shuttle's approach to earth, it’s glide angle changes.

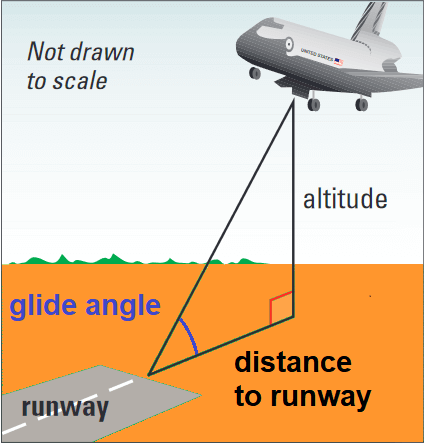
(i) When the shuttle’s altitude is about 15.7 miles, its horizontal distance to the runway is about 59 miles. What is its glide angle ? Round the answer to the nearest tenth.

(ii)  When the space shuttle is 5 miles from the runway, its glide angle is about 19°. Find the shuttle’s altitude at this point in its descent. Round the answer to the nearest tenth.

Solution (i) :

Sketch a right triangle to model the situation. Let x° be the measure of the shuttle’s glide angle.

We can use the tangent ratio and a calculator to find the approximate value of x.

Write ratio.

tan x°  =  opp. / adj.

Substitute.

tan x°  =  15.7 / 59

x  =  tan^-1 (15.7 / 59)

Use calculator to find the value of tan^-1 (15.7 / 59).

x  ≈  14.9

When the space shuttle’s altitude is about 15.7 miles, the glide angle is about 14.9°.

Solution (ii) :

Sketch a right triangle to model the situation. Let h be the altitude of the shuttle. We can use the tangent ratio and a calculator to find the approximate value of h. 

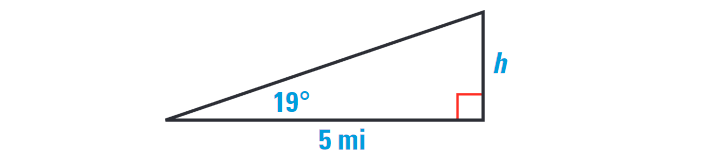
Write ratio.

tan x°  =  opp. / adj.

Substitute.

tan 19°  =  h / 5

Use a calculator.

0.3443  ≈  h / 5

Multiply each side by 5.

5 ⋅ 0.3443  ≈  h

1.7  ≈  h

The shuttle’s altitude is about 1.7 miles.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.