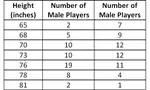
SOLVING QUADRATIC EQUATIONS BY QUADRATIC FORMULA
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The standard form of a quadratic equation is
ax2 + bx + c = 0
Quadratic Formula :
The above formula can be used to solve a quadratic equation in standard form. If the given quadratic equation is not in standard form, convert it to standard form and use the above formula and solve.
Solve each of the following quadratic equations using the quadratic formula.
Example 1 :
x2 – 5x – 24 = 0
Solution :
Comparing the given equation with ax2 + bx + c = 0, we get
a = 1, b = -5, c = -24
Quadratic Formula :
Substitute a = 1, b = -5 and c = -24.
x = 8 or -3
Example 2 :
x2 – 7x + 12 = 0
Solution :
From the given quadratic equation,
a = 1, b = -7, c = 12
Substitute the above values into the quadratic formula.
x = 4 or 3
Example 3 :
x2 – 2x - 5 = 0
Solution :
From the given quadratic equation,
a = 1, b = -2, c = -5
Substitute the above values into the quadratic formula.
Example 4 :
15x2 – 11x + 2 = 0
Solution :
From the given quadratic equation,
a = 15, b = -11, c = 2
Substitute the above values into the quadratic formula.
Example 5 :
x + ¹⁄ₓ = 2½
Solution :
x + ¹⁄ₓ = 2½
x + ¹⁄ₓ = ⁵⁄₂
Multiply both sides by 2x.
2x[x + ¹⁄ₓ] = 2x[⁵⁄₂]
2x2 + 2x(¹⁄ₓ) = 5x
2x2 + 2 = 5x
2x2 - 5x + 2 = 0
From the given quadratic equation,
a = 2, b = -5, c = 2
Substitute the above values into the quadratic formula.
Example 6 :
(x + 3)2 - 81 = 0
Solution :
(x + 3)2 - 81 = 0
(x + 3)(x + 3) - 81 = 0
x2 + 3x + 3x + 9 - 81 = 0
x2 + 6x - 72 = 0
From the given quadratic equation,
a = 1, b = 6, c = -72
Substitute the above values into the quadratic formula.
x = 6 or -12
Example 7 :
Solution :
4x2 - 9x - 43 = 0
From the given quadratic equation,
a = 4, b = -9, c = -43
Substitute the above values into the quadratic formula.
Example 8 :
a(x2 + 1) = x(a2 + 1)
Solution :
a(x2 + 1) = x(a2 + 1)
ax2 + a = xa2 + x
ax2 + a - xa2 - x = 0
ax2 - xa2 - x + a = 0
ax2 - (a2 + 1)x + a = 0
From the given quadratic equation,
a = a, b = -(a2 + 1), c = a
Substitute the above values into the quadratic formula.
Example 9 :
3a2x2 - abx - 2b2 = 0
Solution :
From the given quadratic equation,
a = 3a2, b = -ab, c = -2b2
Substitute the above values into the quadratic formula.
Example 10 :
36x2 – 12ax + (a2 - b2) = 0
Solution :
From the given quadratic equation,
a = 36, b = -12a, c = a2 - b2
Substitute the above values into the quadratic formula.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
SAT Math Problem Solving
Feb 21, 26 01:14 AM
SAT Math Problem Solving -
Digital SAT Math Problems and Solutions (Part - 5)
Feb 20, 26 09:29 PM
Digital SAT Math Problems and Solutions (Part - 5) -
Digital SAT Math Problems and Solutions (Part - 4)
Feb 20, 26 05:55 AM
Digital SAT Math Problems and Solutions (Part - 4)