SOLVING PROBLEMS USING SYSTEMS OF EQUATIONS WORKSHEET

Problem 1 :

Lily and her friends visit the concession stand at a football game. $2 is charged for a sandwich and $1 is charged for a lemonade by the stand. The friends buy a total of 8 items for $11. Say how many sandwiches and how many lemonades they bought.

Problem 2 :

During school vacation, Alex wants to go bowling and to play laser tag. He wants to play 6 total games but needs to figure out how many of each he can play if he spends exactly $20. Each game of bowling is $2 and each game of laser tag is $4.

Detailed Answer Key

Problem 1 :

Lily and her friends visit the concession stand at a football game. $2 is charged for a sandwich and $1 is charged for a lemonade by the stand. The friends buy a total of 8 items for $11. Say how many sandwiches and how many lemonades they bought.

Solution : 

Step 1 :

Let 'x' be the no. of sandwiches and 'y' be the no. of lemonades. 

No. of sandwiches + No. of lemonades  =  Total items

x + y  =  8 -------- (1)

Step 2 : 

Write an equation which represents the money spent on the items.

Cost of 'x' no. of sandwiches  =  2x

Cost of 'y' no. of sandwiches  =  1y

Total cost  =  $11

Then, we have 

2x + 1y  =  11 -------- (2)

Step 3 :

Write the equations (1) and (2) in slope-intercept form. Then graph.

(1) ----- > x + y  =  8 ----- > y  =  -x + 8 

(2) ---- > 2x + 1y  =  11 --- > y  =  -2x + 11 

Graph the equations y = -x + 8 and y = -2x + 11.

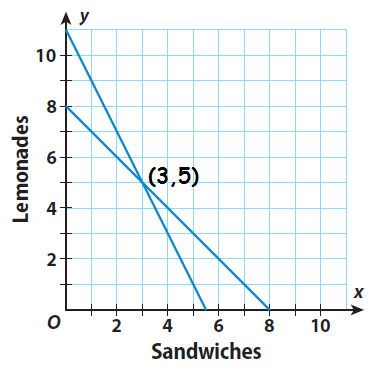
Step 4 :

Look at the graph and identify the solution of the system of equations. Check your answer by substituting the ordered pair into both equations.

The point of intersection of the lines is (3, 5). 

Let us check whether the ordered pair (3, 5) satisfies both the equations. 

Since the ordered pair (3, 5) satisfies both the equations, the solution of the system is (3, 5). 

Step 5 : 

Interpret the solution in the original context.

Lily and her friends bought 3 sandwiches and 5 lemonades.

Problem 2 :

During school vacation, Alex wants to go bowling and to play laser tag. He wants to play 6 total games but needs to figure out how many of each he can play if he spends exactly $20. Each game of bowling is $2 and each game of laser tag is $4.

Solution : 

Step 1 :

Let 'x' be the no. of games Alex bowls and 'y' be the no. of laser tag he plays. 

No. of games he bowls + No. of laser tags  =  Total games

x + y  =  6 -------- (1)

Step 2 : 

Write an equation which represents the money spent on these two items.

Cost of 'x' no. of games he bowls  =  2x

Cost of 'y' no. of laser tags he plays  =  4y

Total cost  =  $20

Then, we have 

2x + 4y  =  20

Divide both sides by 2.

x + 2y  =  10 -------- (2)

Step 3 :

Write the equations (1) and (2) in slope-intercept form. Then graph.

(1) ----- > x + y  =  6 ----- > y  =  -x + 6 

(2) ---- > x + 2y  =  10 --- > y  =  -(1/2)x + 5 

Graph the equations y = -x + 6 and y = -(1/2)x + 5.

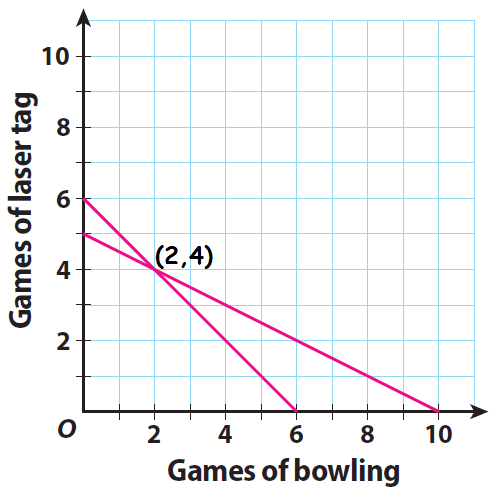
Step 4 :

Look at the graph and identify the solution of the system of equations. Check your answer by substituting the ordered pair into both equations.

The point of intersection of the lines is (2, 4). 

Let us check whether the ordered pair (2, 4) satisfies both the equations. 

Since the ordered pair (2, 4) satisfies both the equations, the solution of the system is (2, 4). 

Step 5 : 

Interpret the solution in the original context.

Alex will bowl 2 games and play 4 games of laser tag.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.