SOLVING LINEAR AND QUADRATIC EQUATIONS

Example 1 :

y  =  x² – 2x + 8 and y  =  x + 6

Solution :

Given equations,

y  =  x² – 2x + 8 -----(1)

y  =  x + 6 -----(2)

By applying y  =  x + 6 in equation (1), we get

x + 6  =  x² – 2x + 8

0  =  x² – 2x + 8 – 6 – x

x² – 3x + 2  =  0

By factorization, we get

(x – 2) (x – 1)  =  0

x  =  2 and x  =  1

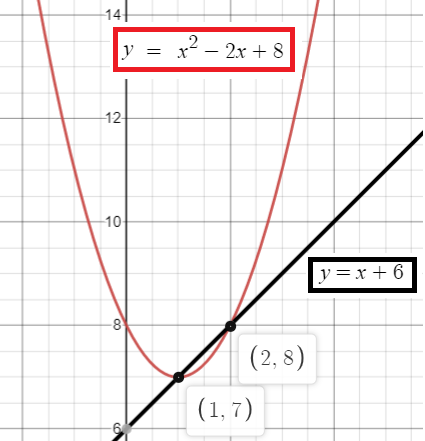
So, the points of intersection are {(2, 8), (1, 7)}

Example 2 :

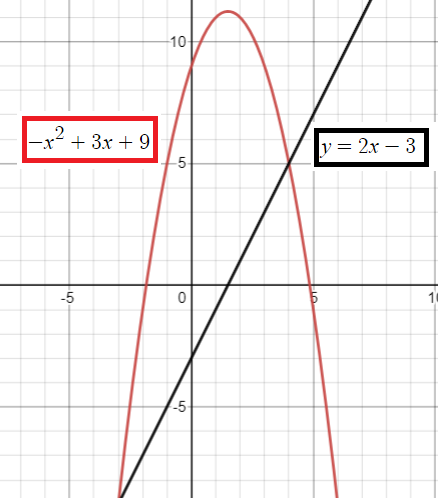
y  =  -x² + 3x + 9 and y  =  2x - 3

Solution :

Given equations,

y  =  -x² + 3x + 9 -----(1)

y  =  2x - 3 -----(2)

By applying y  =  2x - 3 in equation (1), we get

2x - 3  =  -x² + 3x + 9

2x  =  -x² + 3x + 9 + 3

0  =  -x² + 3x + 9 + 3 – 2x

x² – 3x + 2x – 9 - 3  =  0

x² – x – 12  =  0

 By factorization, we get

(x – 4) (x + 3)  =  0

x  =  4 and x  =  -3

So, the points are {(4, 5), (-3, -9)}

Example 3 :

y  =  x² – 3x + 7 and y  =  x + 5

Solution :

Given equations,

y  =  x² – 3x + 7 -----(1)

y  =  x + 5 -----(2)

By applying y  =  x + 5 in equation (1), we get

x + 5  =  x² – 3x + 7

x² – 4x + 2  =  0

Now, we have a quadratic equation form. But there are no factors.

So, we find the x values by using the quadratic formula.

We get,

x  =  [-b ± √(b² – 4ac)]/2a

Here a  =  1, b  =  -4 and c  =  2

x  =  [-(-4) ± √((-4)² – 4(1)(2)]/2(1)

x  =  [4 ± √(16 – 8]/2

x  =  (4 ± √8)/2

x  =  [4 ± √(4×2)]/2

x  =  (4 ± 2√2)/2

x  =  [2(2 ± √2)]/2

x  =  2 ± √2

Now, x  =  2 + √2 and x  =  2 - √2

So, the point of intersections are (2+√2, 7+2) and

(2-√2, 7-√2).

Example 4 :

y  =  x² – 5x + 2 and y  =  x - 7

Solution :

Given equations,

y  =  x² – 5x + 2 -----(1)

y  =  x – 7 -----(2)

By applying y  =  x - 7 in equation (1), we get

x  =  x² – 5x + 2 + 7 + 7 – x

x² – 6x + 9  =  0

By factorization, we get

(x – 3) (x – 3)  =  0

x  =  3

By applying x  =  3 in equation (2), we get

y  =  x – 7

y  =  3 – 7

y  =  -4

If x  =  3 then y  =  -4

So, the solution is (3, -4)

Example 5 :

In the xy-plane, the graph of the equation

y = -x² + 9x - 100

intersects the line

y = c

at exactly one point. What is the value of c?

Solution :

y = -x² + 9x - 100

y = c

-x² + 9x - 100 = c

-x² + 9x - 100 - c = 0

a = -1, b = 9 and c = -(100 + c)

Since the parabola and the line is intersecting at one point, it should satisfy the condition

b² - 4ac = 0

9² + 4(-1)(100 + c) = 0

9² - 4(100 + c) = 0

81 = 400 - 4c

81 - 400 = -4c

-319 = -4c

c = 319/4

So, the value of c is 319/4.

Example 6 :

x + 7 = 10

(x + 7)² = y

Which ordered pair (x, y) is a solution to the given system of equations.

a)  (3, 100)     b)  (3, 3)     c) (3, 10)      d) (3, 70)

Solution :

x + 7 = 10 ------(1)

Solving this, x = 10 - 7

x = 3

Applying the value of x

(x + 7)² = y ------(2)

(3 + 7)² = y

y = 10²

y = 100

So, the solution is (3, 100). Option a is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.