SOLVING EQUATIONS WITH VARIABLES ON BOTH SIDES WORKSHEET WITH ANSWER KEY
Problem 1 :
Solve for r :
6r + 7 = 13 + 7r
Problem 2 :
Solve for x :
-7x - 3x + 2 = -8x - 8
Problem 3 :
Solve for n :
4n - 40 = 7(-2n + 2)
Problem 4 :
Solve for k :
5(k - 3) - 7(6 - k) = 24 - 3(8 - k) - 3
Problem 5 :
Solve for x :
3(1 - 3x) = 2(-4x + 7)
Problem 6 :
Solve for x :
⁴ˣ⁄₅ - ⁷⁄₄ = ˣ⁄₅ + ˣ⁄₄
Problem 7 :
Solve for x :
⁽ˣ ⁻ ²⁾⁄₂ + ⁽ˣ ⁺ ¹⁰⁾⁄₉ = 5
Problem 8 :
Solve for x :
(x + 1)(2x + 1) = (x + 3)(2x + 3) - 14
Problem 9 :
Solve the following equation :
½(8y - 6) = 5y - (y + 3)
Problem 10 :
Solve the following equation :
2(1 - x) + 5x = 3(x + 1)

Answers
1. Answer :
6r + 7 = 13 + 7r
Subtract 6r from each side.
7 = 13 + r
Subtract 13 from each side.
-6 = r
2. Answer :
-7x - 3x + 2 = -8x - 8
Simplify.
-10x + 2 = -8x - 8
Add 10x to each side.
2 = 2x - 8
Add 8 to each side.
10 = 2x
Divide each side by 2.
5 = x
3. Answer :
4n - 40 = 7(-2n + 2)
Use distributive property.
4n - 40 = -14n + 14
Add 14n to each side.
18n - 40 = 14
Add 40 to each side.
18n = 54
Divide each side by 18.
n = 3
4. Answer :
5(k - 3) - 7(6 - k) = 24 - 3(8 - k) - 3
Use distributive property.
5k - 15 - 42 + 7k = 24 - 24 + 3k - 3
Simplify.
12k - 57 = 3k - 3
Subtract 3k from each side.
9k - 57 = -3
Add 57 to each side.
9k = 54
Divide each side by 9.
k = 6
5. Answer :
3(1 - 3x) = 2(-4x + 7)
Use distributive property.
3 - 9x = -8x + 14
Add 9x to each side.
3 = x + 14
Subtract 14 from each side.
-11 = x
6. Answer :
⁴ˣ⁄₅ - ⁷⁄₄ = ˣ⁄₅ + ˣ⁄₄
The least common multiple of the denominators in the equation is 4 × 5 = 20 and we proceed as follows :
20(⁴ˣ⁄₅ - ⁷⁄₄) = 20(ˣ⁄₅ + ˣ⁄₄)
20(⁴ˣ⁄₅) - 20(⁷⁄₄) = 20(ˣ⁄₅) + 20(ˣ⁄₄)
16x - 35 = 4x + 5x
16x - 35 = 9x
Subtract 9x from each side.
7x - 35 = 0
Add 35 to each side.
7x = 35
Divide each side by 7.
x = 5
7. Answer :
⁽ˣ ⁻ ²⁾⁄₂ + ⁽ˣ ⁺ ¹⁰⁾⁄₉ = 5
The least common multiple of the denominators in the equation is 2 × 9 = 18 and we proceed as follows :
18(⁽ˣ ⁻ ²⁾⁄₂ + ⁽ˣ ⁺ ¹⁰⁾⁄₉) = 18(5)
18(⁽ˣ ⁻ ²⁾⁄₂) + 18(⁽ˣ ⁺ ¹⁰⁾⁄₉) = 90
9(x - 2) + 2(x + 10) = 90
9x - 18 + 2x + 20 = 90
11x + 2 = 90
Subtract 2 from each side.
11x = 88
Divide each side by 11.
x = 8
8. Answer :
(x + 1)(2x + 1) = (x + 3)(2x + 3) - 14
Simplify.
2x2 + 3x + 1 = 2x2 + 9x + 9 - 14
2x2 + 3x + 1 = 2x2 + 9x - 5
Subtract 2x2 from each side.
3x + 1 = 9x - 5
Subtract 3x from each side.
1 = 6x - 5
Add 5 to each side.
6 = 6x
Divide each side by 6.
1 = x
9. Answer :
½(8y - 6) = 5y - (y + 3)
Simplify both sides.
½(8y) - ½(6) = 5y - (y + 3)
4y - 3 = 5y - y - 3
4y - 3 = 4y - 3
Subtract 4y from each side.
-3 = -3
The above result is true. Because the result we get at the last step is true, the given equation has infinitely has many solutions.
10. Answer :
2(1 - x) + 5x = 3(x + 1)
Simplify both sides.
2 - 2x + 5x = 3x + 3
2 + 3x = 3x + 3
Subtract 3x from each side.
2 = 3
The above result is false. Because 2 is not equal to 3. Because the result we get at the last step is false, the given equation has no solution.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 188)
Jun 17, 25 02:26 AM
Digital SAT Math Problems and Solutions (Part - 188) -
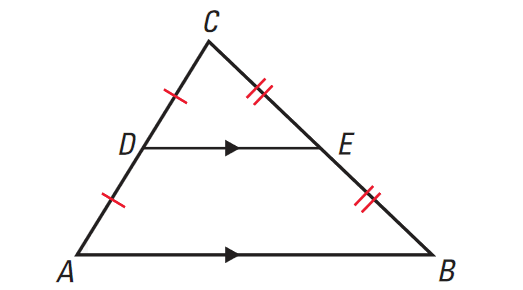
Midsegment Theorem
Jun 15, 25 09:40 PM
Midsegment Theorem - Concept - Solved Problems -
Digital SAT Math Problems and Solutions (Part - 187)
Jun 14, 25 09:07 AM
Digital SAT Math Problems and Solutions (Part - 187)