SOLVING AND GRAPHING INEQUALITIES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If an inequality is in the form
(x < a) or (x > a) or (x ≤ a) or (x ≥ a),
where a is a constant, we can easily sketch the graph of the inequality.
In case, the inequality is in the form
ax + b < bx + d,
where a, b and d are constants, we have to solve for x and sketch the graph.
Solving Inequalities
Step 1 :
Same number may be added or subtracted from both sides of an inequality without changing the sign of inequality.
Step 2 :
Both sides of an inequality can be multiplied or divided by same positive real number without changing the sign of inequality. However the sign of inequality is revered when both sides of an inequality are multiplied or divided by a negative number.
Step 3 :
Any term of an inequality may be taken to the other sides with its sign changed without affecting the sign of inequality.
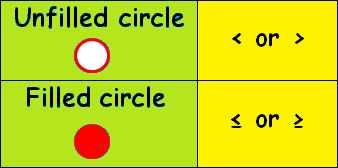
Graphing Inequalities
In graphing inequalities in one variable on a number line, we have to follow the steps given below.
Step 1 :
If we have one of the signs like < (less than) or > (greater than), we have to use the unfilled circle.
Step 2 :
If we have one of the signs like ≤ (less than or equal to) or ≥ (greater than or equal to), we have to use the filled circle.
Example 1 :
Solve the following linear inequality and graph.
2x - 4 ≤ 0
Solution :
2x - 4 ≤ 0
Add 4 on both sides
2x - 4 + 4 ≤ 0 + 4
2x ≤ 4
Divide by 2 on both sides
2x/2 ≤ 4/2
x ≤ 2
So, any real number less than or equal to 2 is a solution of the given equation.

The solution set of the given inequality is (-∞, 2].
Example 2 :
Solve the following linear inequality and graph.
-3x + 12 < 0
Solution :
-3x + 12 < 0
Subtract 12 on both sides
-3x + 12 - 12 < 0 - 12
-3x < -12
Divide by -4 on both sides
-3x/(-3) < -12/(-3)
x < 4
So, any real number less 4 is a solution of the given equation.

The solution set of the given inequality is (-∞, 2].
Example 3 :
Solve the following linear inequality and graph.
4x - 12 ≥ 0
Solution :
4x - 12 ≥ 0
Add 12 on both sides
4x - 12 + 12 ≥ 0 + 12
4x ≥ 12
Divide by 4 on both sides
4x/4 ≥ 12/4
x ≥ 3
So, any real number greater than or equal to 3 is a solution of the given equation.

The solution set of the given inequality is [3, ∞).
Example 4 :
Solve the following linear inequality and graph.
7x + 9 > 30
Solution :
7x + 9 > 30
Subtract 9 on both sides
7x + 9 - 9 > 30 - 9
7x > 21
Divide by 7 on both sides
7x/7 > 21/7
x > 3
So, any real number greater than 3 is a solution of the given equation.

The solution set of the given inequality is (3, ∞).
Example 5 :
Solve the following linear inequality and graph.
5x - 3 < 3x + 1
Solution :
5x - 3 < 3x + 1
Subtract 3x on both sides
5x - 3 - 3x < 3x + 1 - 3x
2x - 3 < 1
Add 3 on both sides
2x - 3 + 3 < 1 + 3
2x < 4
Divide by 2 on both sides
2x/2 < 4/2
x < 2
So, any real number lesser than 2 is a solution of the given equation.
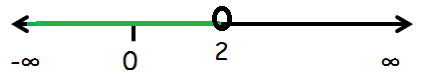
The solution set of the given inequality is (2, ∞).
Example 6 :
Solve the following linear inequality and graph.
3x + 17 ≤ 2(1 - x)
Solution :
3x + 17 ≤ 2(1 - x)
3x + 17 ≤ 2 - 2x
Add 2x on both sides
3x + 2x + 17 ≤ 2 - 2x + 2x
5x + 17 ≤ 2
Subtract 17 on both sides
5x + 17 - 17 ≤ 2 - 17
5x ≤ -15
Divide by 5 on both sides
5x/5 ≤ -15/5
x ≤ -3
So, any real number lesser than or equal to -3 is a solution of the given equation.
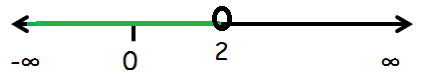
The solution set of the given inequality is (-∞ , -3].
Example 7 :
Solve the following linear inequality and graph.
2(2x + 3) - 10 ≤ 6 (x - 2)
Solution :
2(2x + 3) - 10 ≤ 6 (x - 2)
4x + 6 - 10 ≤ 6 x - 12
4x - 4 ≤ 6 x - 12
Subtract 6x on both sides
4x - 4 - 6x ≤ 6 x - 12 - 6x
-2x - 4 ≤ - 12
Add 4 on both sides
-2x - 4 + 4 ≤ - 12 + 4
-2x ≤ - 8
Divide by -2 on both sides
-2x / (-2) ≤ - 8 / (-2)
x ≤ 4
So, any real number lesser than or equal to 4 is a solution of the given equation.

The solution set of the given inequality is (-∞ , 4].
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations -
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos -
Times Table Shortcuts
Dec 30, 25 07:14 PM
Times Table Shortcuts - Concept - Examples
