SLOPE OF A LINE JOINING TWO POINTS WORKSHEET

Problem 1 :

Find the slope of a straight joining the two points (3, -2) and (-1, 4).

Problem 2 :

Find the slope of a straight joining the two points (5, -2) and (4, -1).

Problem 3 :

Find the slope of a straight joining the two points (-2, -1) and (4, 0).

Problem 4 :

Find the slope of a straight joining the two points (1, 2) and (-4, 5).

Problem 5 :

If the slope of a line joining the two points (1, -2) and (3, k) is 5, find the value of k.

Problem 6 :

If the line that passes through (4, 3) and (-5, r) has a slope of -1, what is the value of r?

Problem 7 :

If the line that passes through (a, 7) and (1, a) has a slope of -⁵⁄₉, what is the value of a?

Problem 8 :

The graph of the linear function f passes through the points (a, 1) and (1, b) in the xy-plane. If the slope of the graph of f is 1, which of the following is true?

(A)  a - b = 1

(B)  a + b = 1

(C)  a - b = 2

(D)  a + b = 2

Problem 9 :

Find the slope of the line in xy-plane shown below.

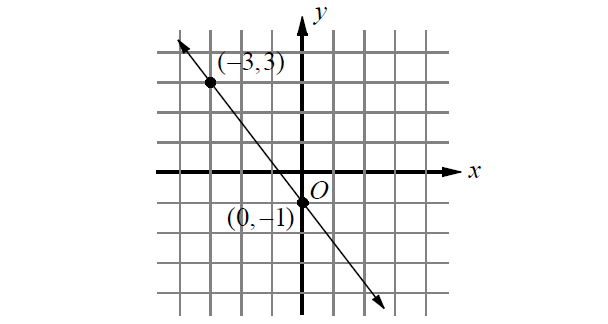
Problem 10 :

Find the slope of the line in xy-plane shown below.

Question 11 :

If the points A(2, 2), B(–2, –3), C(1, –3) and D(x, y) form a parallelogram then find the value of x and y.

Question 12 :

Let A(3, -4), B(9, -4), C(5, -7) and D(7, -7) . Show that ABCD is a trapezium.

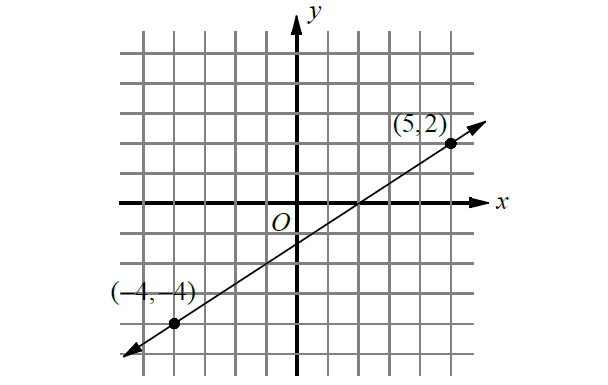
Answers

1. Answer :

(3, -2) and (-1, 4)

Formula to find the slope of a line joining two points :

Substitute (x₁, y₁) = (3, -2) and (x₂, y₂) = (-1, 4).

2. Answer :

(5, -2) and (4, -1)

Formula :

Substitute (x₁, y₁) = (5, -2) and (x₂, y₂) = (4, -1).

m = -1

3. Answer :

(-2, - 1) and (4, 0)

Formula :

Substitute (x₁, y₁) = (-2, -1) and (x₂, y₂) = (4, 0).

4. Answer :

(1, 2) and (-4, 5)

Formula :

Substitute (x₁, y₁) = (1, 2) and (x₂, y₂) = (-4, 5).

5. Answer :

slope = 5

Substitute (x₁, y₁) = (1, -2) and (x₂, y₂) = (3, k).

Multiply both sides by 2.

k + 2 = 10

Subtract 2 from both sides.

k = 8

6. Answer :

slope = -1

Substitute (x₁, y₁) = (4, 3) and (x₂, y₂) = (-5, r).

Multiply both sides by -9.

r - 3 = 9

Add 3 to both sides.

r = 12

7. Answer :

Substitute (x₁, y₁) = (a, 7) and (x₂, y₂) = (1, a).

By cross-multiplication,

9(a - 7) = -5(1 - a)

Use the Distributive Property.

9a - 63 = -5 + 5a

Subtract 5a from both sides.

4a - 63 = -5

Add 63 to both sides.

4a = 58

Divide both sides by 4.

a = ⁵⁸⁄₄

a = ²⁹⁄₂

8. Answer :

slope = 1

Substitute (x₁, y₁) = (a, 1) and (x₂, y₂) = (1, b).

Multiply both sides by (1 - a).

b - 1 = 1 - a

Add a to both sides.

a + b - 1 = 1

Add 1 to both sides.

a + b = 2

Therefore, the corect answer is option (D).

9. Answer :

Measure the rise and run.

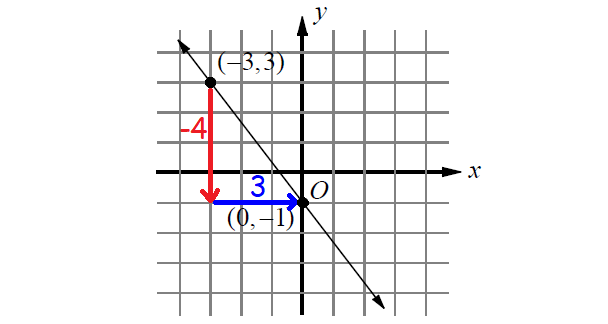
For the above line,

rise = -4

run = 3

Then,

slope = ʳⁱˢᵉ⁄ᵣᵤₙ

= -⁴⁄₃

10. Answer :

Measure the rise and run.

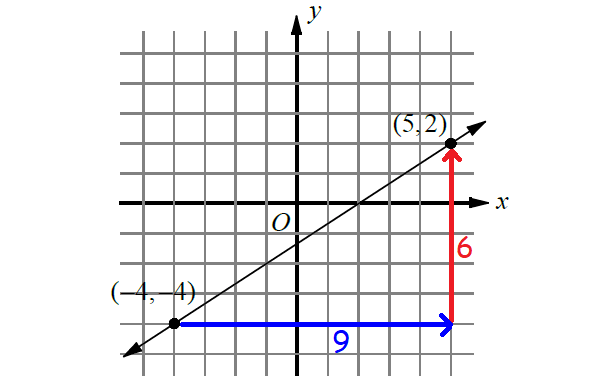
For the above line,

rise = 6

run = 9

Then,

slope = ʳⁱˢᵉ⁄ᵣᵤₙ

= ⁶⁄₉

= ⅔

11. Answer :

Since the given points form a parallelogram,

Slope of AB = Slope of CD

Slope of BC = Slope of DA

A(2, 2), B(–2, –3), C(1, –3) and D(x, y)

(1) = (2) :

⁵⁄₄ = ⁽ʸ ⁺ ³⁾⁄₍ₓ ₋ ₁₎

5(x - 1) = 4(y + 3)

5x - 5 = 4y + 12

5x - 4y = 12 + 5

5x - 4y = 17 -----(5)

(3) = (4) :

0 = ⁽ʸ ⁻ ²⁾⁄₍ₓ ₋ ₂₎

0 = y - 2

2 = y

Substitute y = 2 into (5).

5x - 4(2) = 17

5x - 8 = 17

5x = 25

x = 5

Therefore,

(x, y) = (5, 2)

12. Answer :

A(3, -4), B(9, -4) , C(5, -7) and D(7, -7)

A trapezium always contains two parallel sides and two non parallel sides.

Slope of AB = (-4 + 4)/(9 - 3)

= 0/6

= 0

Slope of BC = (-7 + 4)/(5 - 9)

= -3/-4

= 3/4

Slope of CD = (-7 + 7)/(7 - 5)

= 0/2

= 0

Slope of DA = (-7 + 4)/(7 - 3)

= -3/4

From the above working, we have

Slope of AB = Slope of CD ----> AB and CD are parallel

Slope of BC ≠ Slope of DA ----> BC and DA are not parallel

Therefore, ABCD is a trapezium.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.