SEGMENT LENGTHS IN CIRCLES WORKSHEET

Problem 1 :

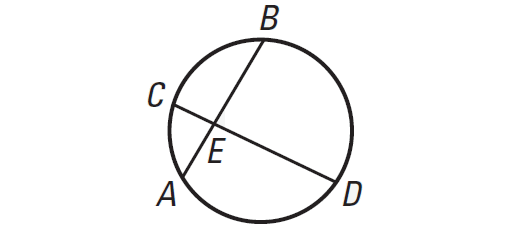
In the diagram shown below, prove the following. 

EA ⋅ EB  =  EC ⋅ ED

Problem 2 :

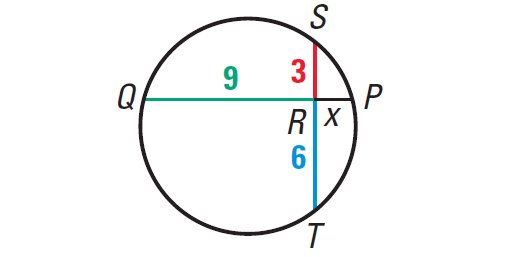
Chords ST and PQ intersect inside the circle.  Find the value of x.

Problem 3 :

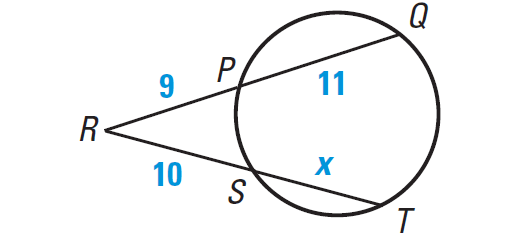
Find the value of x in the diagram shown below. 

Problem 4 :

Find the value of x in the diagram shown below. 

Problem 5 :

You are standing at point C,  about 8 feet from a circular aquarium tank.  The distance from you to a point of tangency on the tank is about 20 feet.  Estimate the radius of the tank.

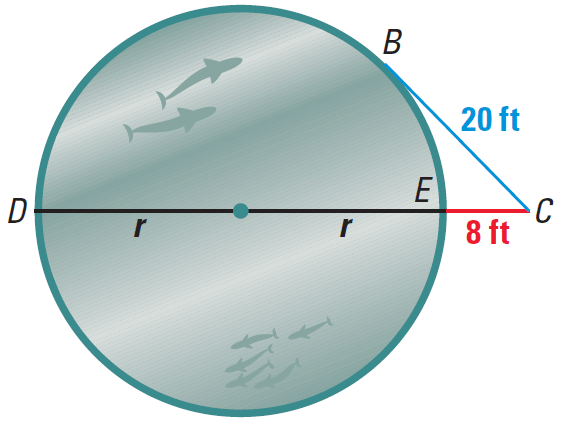
Answers

Problem 1 :

In the diagram shown below, prove the following. 

EA ⋅ EB  =  EC ⋅ ED

Answer :

We can use similar triangles to prove the Theorem. 

Given : AB, CD are chords that intersect at E.

To Prove : EA · EB =  EC · ED

Draw DB and AC in the above diagram.

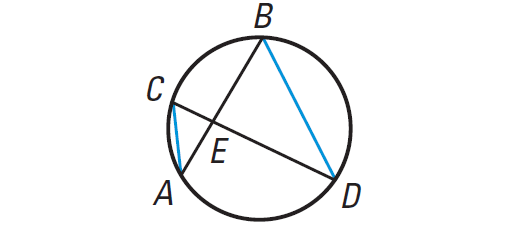
Because m∠C and m∠B intercept the same are ∠C  ≅  ∠B.  Likewise  ∠A  ≅  ∠D. 

By the AA Similarity Postulate.  ∆AEC ∼ ∆DEB. 

So, the lengths of corresponding sides are proportional.

EA/ED  =  EC/EB

EA ⋅ EB  =  EC ⋅ ED

Problem 2 :

Chords ST and PQ intersect inside the circle.  Find the value of x.

Answer :

Using Theorem, we have 

RQ · RP  =  RS · RT

Substitute.

9 · x  =  3 · 6

9x  =  18

Divide each side by 9. 

9x/9  =  18/9

x  =  2

Problem 3 :

Find the value of x in the diagram shown below. 

Answer :

Using Theorem, we have

RP · RQ  =  RS · RT

Substitute. 

9 · (11 + 9)  =  10 · (x + 10)

Simplify. 

180  =  10x + 100

Subtract 100 from each side. 

80  =  10x

Divide each side by 10.

80/10  =  10x/10

8  =  x

Problem 4 :

Find the value of x in the diagram shown below. 

Answer :

Using Theorem, we have

(BA)²  =  BC · BD

Substitute. 

6²  =  x · (x + 5)

Simplify. 

36  =  x² + 5x

Subtract 36 from each side. 

0  =  x² + 5x - 36

or

x² + 5x - 36  =  0

Factor. 

(x + 9)(x - 4)  =  0

x + 9  =  0        or        x - 4  =  0

x  =  - 9        or        x  =  4

We can use only positive value for x. because lengths cannot be negative. 

So, we have

x  =  4

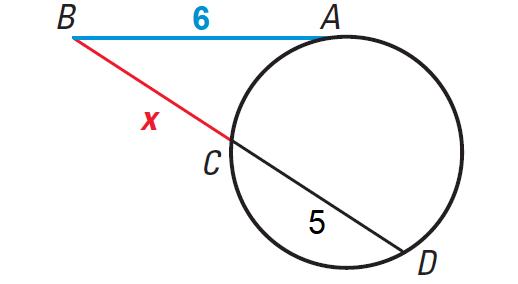
Problem 5 :

You are standing at point C,  about 8 feet from a circular aquarium tank.  The distance from you to a point of tangency on the tank is about 20 feet.  Estimate the radius of the tank.

Answer :

Using Theorem, we have

(CB)²  =  CE · CD

Substitute.

20²  ≈  8 · (2r + 8)

Simplify.

400  ≈  16r + 64

Subtract 64 from each side. 

336  ≈  16r

Divide each side by 16. 

336/16  ≈  16r/16

21  ≈  r

Hence, the radius of the tank is about 21 feet. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.