SAT MATH - SOLVING EQUATIONS

Problem 1 :

If (⅚)x = ⅘, what is the value of x?

(A)  ³⁄₂

(B)  ⅔

(C)  ²⁴⁄₂₅

(D)  ²⁵⁄₂₄

Solution :

(⅚)x = ⅘

Multiply both sides by 6.

5x = ²⁴⁄₅

Divide both sides by 5.

x = ²⁴⁄₂₅

Therefore, the correct answer is option (C).

Problem 2 :

When one half of the number n is decreased by 4, the result is -6. What is three times n added to 7?

(A)  -7

(B)  -5

(C)  -3

(D)  -1

Solution :

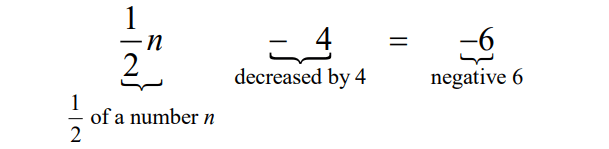
(½)n - 4 = -6

Add 4 to both sides.

(½)n = -2

Multiply both sides by 2.

n = -4

Three times n added to 7 :

= 3n + 7

Substitute n = -4.

= 3(-4) + 7

= -12 + 7

= -5

Therefore, the correct answer is option (B).

Problem 3 :

If 4 - 7x is 5 less than 23, what is the value of 3x? 

(A)  -12

(B)  -9

(C)  -6

(D)  -3

Solution :

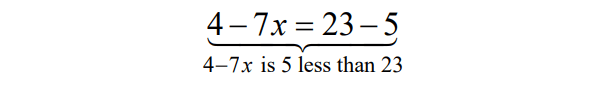
4 - 7x = 23 - 5

4 - 7x = 18

Subtract 4 from both sides.

-7x = 14

Divide both sides by -7.

x = -2

3(x) = 3(-2)

3x = -6

Therefore, the correct answer is option (C).

Problem 4 :

The above equation gives pressure P, which is exerted by a fluid that is forced to stop moving. The pressure depends on the initial force F, and the speed of the fluid v. Which of the following expresses the square of the velocity in terms of the pressure and the force?

Solution :

Therefore, the correct answer is option (D).

Problem 5 :

One half of the number n increased by 10 is the same as four less than twice the number. 

Which of the following equations represents the statement above?

(A)  (½)(n + 10) = 2(n - 4)

(B)  (½)n + 10 = 2(n - 4)

(C)  (½)n + 10 = 2n - 4

(D)  (½)(n + 10) = 2n - 4

Solution :

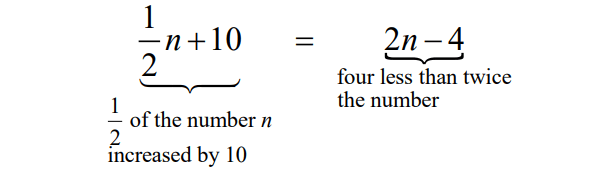
Therefore, the correct answer is option (C).

Problem 6 :

If a is b less than one-half of c, what is b in terms of a and c?

(A)  (½)c - a

(B)  a - (½)c

(C)  2a - c

(D)  c -  2a

Solution :

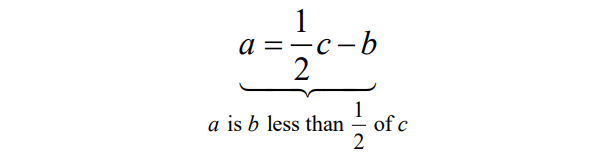
a = (½)c - b

a + b = (½)c

b = (½)c - a

Therefore, the correct answer is option (A).

Problem 7 :

If x = 1 - y and 3x = 8 - 5y, what is the value of x?

(A)  -2

(B)  -³⁄₂

(C)  -½

(D)  -⁵⁄₂

Solution :

x = 1 - y ----(1)

3x = 8 - 5y ----(2)

Substitute x = 1 - y into (2).

3(1 - y) = 8 - 5y

3 - 3y = 8 - 5y

2y = 5

y = ⁵⁄₂

Substitute y = ⁵⁄₂ into (1).

x = 1 - ⁵⁄₂

x = -³⁄₂

Therefore, the correct answer is option (B).

Problem 8 :

The quotient of a number and five equals nine less than one half of the number. What is the number?

(A)  -20

(B)  -10

(C)  20

(D)  30

Solution :

Let x be the number.

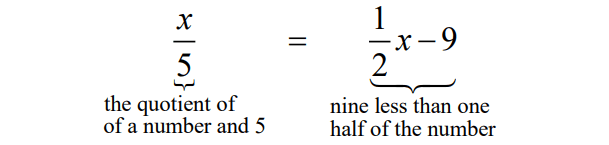
ˣ⁄₅ = (½)x - 9

The least common multiple of (5, 2) = 10.

Multiply both sides by 10 to get rid of the denominators 5 and 2.

10(ˣ⁄₅) = 10[(½)x - 9]

2x = 10[(½)x] - 10(9)

2x = 5x - 90

-3x = -90

x = 30

Therefore, the correct answer is option (D).

Problem 9 :

If ᵃ⁄b = 1, what is the value of (a - b)?

Solution :

ᵃ⁄b = 1

a = b

a - b = 0

Problem 10 :

When an object is thrown from the ground into the air with an initial upward speed of v₀ meters per second, the speed v, in meters per second, is given by the equation v = v₀ - 9.8t, where t is the time in seconds. The speed of an object becomes 0 when the object reaches its maximum height. If an object is thrown upward with an initial speed of 14 meters per sec, how many seconds does it take to reach its maximum height? (Round your answer to the nearest hundredth of a second.)

Solution :

v = v₀ - 9.8t

Given : Initial speed is 14 meters per sec.

Substitute v₀ = 14 into the given equation.

v = 14 - 9.8t

As the object moves upward, its speed decreases  continuously and becomes 0 as it reaches its maximum height.

At the maximum height, v = 0.

0 = 14 - 9.8t

9.8t = 14

t ≈ 1.43

Therefore, the object takes about 1.43 seconds to reach its maximum height.

Problem 11 :

When an object is dropped from a height of s feet above the ground, the height h of the object is given by the equation h = -16t² + s, where t is the time in seconds after the object has dropped. If an object is dropped from a height of 144 feet above the ground, how many seconds will it take to hit the ground?

Solution :

h = -16t² + s

Given : The object is dropped from a height of 144 feet above the ground

Substitute s = 144 into the given equation.

h = -16t² + 144

When the object hits the ground, the height is 0.

Substitute h = 0.

0 = -16t² + 144

16t² = 144

t² = 9

t = √9

t = ±3

t = -3  or  t = 3

Time can not be negative, so t = 3.

Therefore, the object will take 3 seconds to hit the ground.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.