SAT MATH - SLOPE INTERCEPT FORM AND POINT SLOPE FORM

Solved Problems

Problem 1 :

The graph of a linear equation is shown on the diagram below.

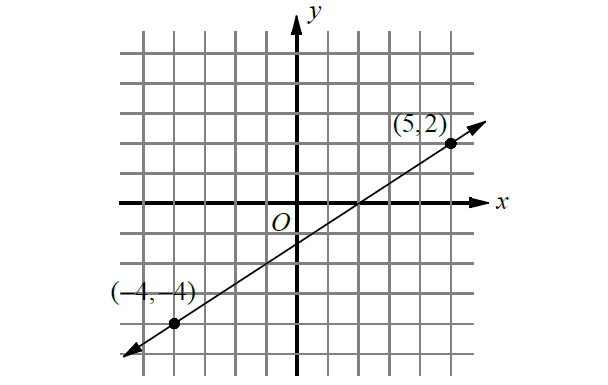
(a) Find the slope of the line on the graph.

(b) Write the equation of the line in slope-intercept form.

(c) Write the equation of the line in point-slope form using the point (5, 2).

Solution :

Part (a) :

Formula to find the slope of a line joining two points :

Substitute (x₁, y₁) = (-4, -4) and (x₂, y₂) = (5, 2).

Part (b) :

Slope-intercept form equation of a line :

y = mx + b

Substitute m = ⅔.

y = (⅔)x + b

To find the value of b, substitute one of the points on the line into the equation.

Substitute (x, y) = (5, 2).

2 = (⅔)(5) + b

2 = ¹⁰⁄₃ + b

2 - ¹⁰⁄₃ = b

-⁴⁄₃ = b

Therefore, slope-intercept form equation of the given line :

y = (⅔)x - ⁴⁄₃

Part (c) :

Point-slope form equation of a line :

y - y₁ = m(x - x₁)

Substitute m = ⅔ and (x₁, y₁) = (5, 2).

y - 2 = (⅔)(x - 5)

Problems 2-4 : Refer to the following information.

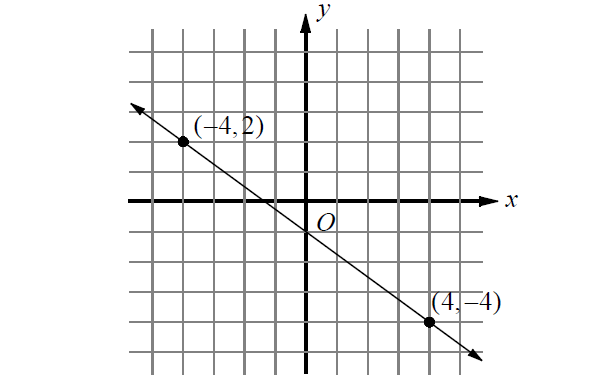
The graph of a linear equation is shown on the diagram below.

Problem 2 :

Which of the following is the equation of the line in point-slope form?

(A)  y + 4 = (-⁴⁄₃)(x - 4)

(B)  y - 4 = (-⁴⁄₃)(x + 4)

(C)  y - 2 = (-¾)(x + 4)

(D)  y + 2 = (-¾)(x -  4)

Solution :

Formula to find the slope of a line joining two points :

Substitute (x₁, y₁) = (-4, 2) and (x₂, y₂) = (4, -4).

Equation of the line in point-slope form :

y - y₁ = m(x - x₁)

y - y₁ = (-¾)(x - x₁)

Therefore, the correct answer is option (C).

Problem 3 :

Which of the following is the equation of the line in slope-intercept form?

(A)  y = (-¾)x + 1

(B)  y = (-¾)x - 1

(C)  y = (-⁴⁄₃)x + 1

(D)  y = (-⁴⁄₃)x - 1 

Solution :

Equation of a line in slope-intercept form :

y = mx + b

We already know the slope of the line, that is m = -¾.

y = (-¾)x + b

Substitute one of the points on the line to find the value of b.

Substitute (x, y) = (-4, 2).

2 = (-¾)(-4) + b

2 = (-3)(-1) + b

2 = 3 + b

-1 = b

Equation of the given line in slope-intercept form :

y = (-¾)x - 1

Therefore, the correct answer is option (B).

Problem 4 :

Which of the following is the equation of the line in standard form?

(A)  4x - 3y = -4 

(B)  4x + 3y = -4

(C)  3x - 4y = -4

(D)  3x + 4y = -4 

Solution :

Consider the equation of the line in slope-intercept form found in problem 3 above.

y = (-¾)x - 1

Multiply both sides by 4.

4y = 4[(-¾)x - 1]

4y = 4[(-¾)x] - 4

4y = -3x - 4

Add 3x to both sides.

3x + 4y = -4

Therefore, the correct answer is option (D).

Problem 5 :

Which of the following is the equation of the line that passes through point (4, -1) and has slope -2?

(A)  x + 2y - 2 = 0 

(B)  x - 2y - 6 = 0

(C)  2x - y - 9 = 0 

(D)  2x + y - 7 = 0 

Solution :

Equation of a line in slope-intercept form :

y = mx + b

Given : Slope m = -2.

y = -2x + b

Substitute (x, y) = (4, -1).

-1 = -2(4) + b

-1 = -8 + b

7 = b

Equation of the given line :

y = -2x + 7

Add 2x to both sides.

2x + y = 7

Subtract 7 from both sides.

2x + y - 7 = 0

Therefore, the correct answer is option (D).

Problem 6 :

A cab service charges a fixed rate of $25 and $2.50 per mile. Write an equation in slope-intercept form that models this situation. Use the equation to find the total cost for a 25-miles trip. 

Solution :

Let y be the total cost for travelling x miles.

The equation in slope-intercept form that models this situation is

y = 2.5x + 30

To find the total cost for an 25-miles trip, substitute x = 25 into the above equation.

y = 3(25) + 30

y = 75 + 30

y = 105

The total cost for a 25-miles trip is $105.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.