SAT MATH QUESTIONS WITH ANSWERS
(Part - 2)

Question 1 :

Find one possible integer value of x :

Answer :

Multiply by 6.

Add 2.

The integer values we have between 6.5 and 8.75 are 7 and 8.

One possible integer value of x is 7 or 8.

Question 2 :

Find the value of (3x + 4).

Answer :

Question 3 :

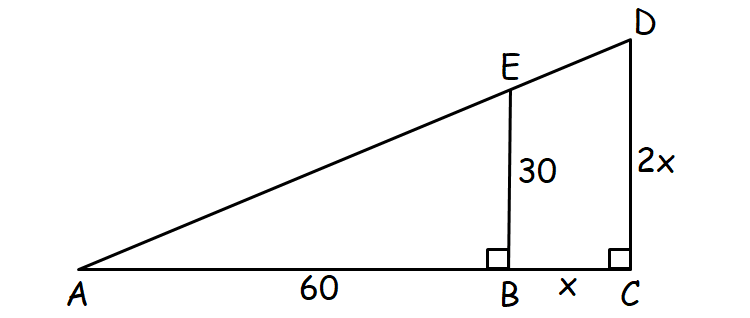
In the figure above, right triangles ACD and ABE are similar. What is the value of x?

Answer :

Since the right triangles ACD and ABE are similar, the corresponding sides are proportional. That is, the ratios of the corresponding sides are equal.

Multiply both sides by 60.

Question 4 :

Which of the following inequalities gives the solution set for the above inequality?

(A) -5 ≤ x ≤ 4

(B) -4 ≤ x ≤ 5

(C) x ≤ -5  or  x ≥ 4

(C) x ≤ -4  or  x ≥ 5

Answer :

In the above inequality, we have (x + 4) inside the square root. If (x + 4) is negative, √(x + 4) will be imaginary. So, (x + 4) can be equal to zero or greater than zero.

0 ≤ x + 4

-4 ≤ x ----(1)

Since we have positive values on both sides of the given inequality, squaring both sides will not affect the inequality sign ≥.

9 ≥ x + 4

5 ≥ x

x ≤ 5 ----(2)

Combining (1) and (2),

-4 ≤ x ≤ 5

Therefore, option (B) is correct.

Question 5 :

A librarian is packing books to put into storage. She packs books at a rate of 20 per minute. If she needs 12 boxes to pack 780 books, how many minutes will it take her to fill b boxes of books?

Answer :

Given : Librarian packs books at a rate of 20.

Number of books packed in 1 minute = 20

Time required to pack 780 books :

= ⁷⁸⁰⁄₂₀

= 39 minutes

Since 780 books are packed in 12 boxes, time required to pack 12 boxes is also 39 minutes.

Time required to pack 1 box :

= ³⁹⁄₁₂

= ¹³⁄₄

Time required to pack b boxes :

= (¹³⁄₄)b

= ¹³^b⁄₄

Therefore, option (D) is correct.

Question 6 :

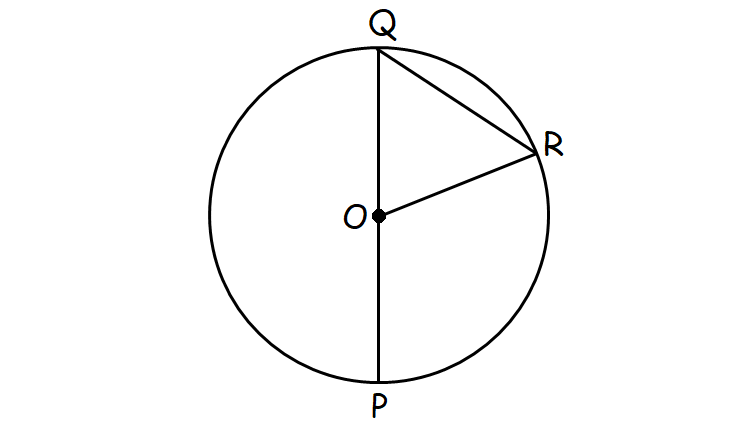
In circle above, the measure of angle QOR is equal to half of the measure of angle POR. If circle O has a radius of r, what is the length of the chord?

(A) r

(B) √2r

(B) √3r

(C) 2r

Answer :

Given : Measure of angle QOR is equal to half of the measure of angle POR.

Let 2x be the angle measure of POR. Then the angle measure of QOR is x.

Angles POR and QOR form a linear pair.

m∠POR + m∠QOR = 180°

2x + x = 180°

3x = 180°

x = 60°

OQ and OR are the radii of the circle.

OQ = OR

Since OQ = OR in triangle OQR inside the circle,

m∠OQR = m∠ORQ

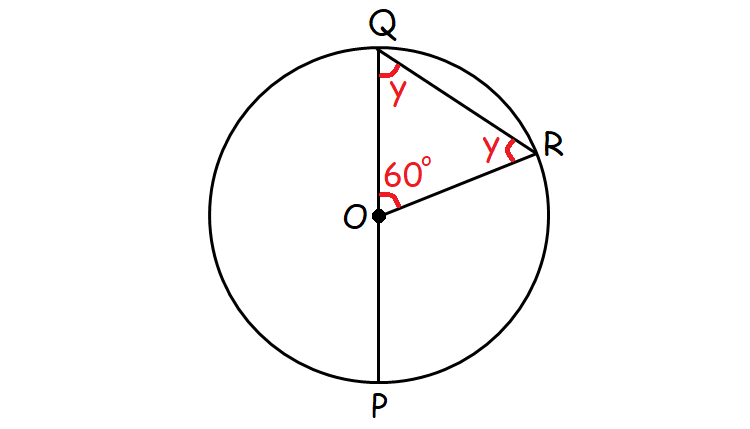
In triangle OQR,

y + y + 60° = 180°

2y + 60° = 180°

2y = 120°

y = 60°

So, triangle OQR is an equilateral triangle.

OQ = OR = QR = r

Therefore, option (A) is correct.

Question 7 :

If (x + 3)² < 100 and x = -2c, what is the largest possible integr value of c?

Answer :

(x + 3)² < 100

(x + 3)² - 100 < 0

(x + 3)² - 10 < 0

Using algebraic identity a² - b² = (a + b)(a - b),

[(x + 3) + 10][(x + 3) - 10] < 0

(x + 3 + 10)(x + 3 - 10) < 0

(x + 13)(x - 7) < 0

Let (x + 13)(x - 7) = 0.

x = -13 or x = 7

From the above real number line, we can have the following three intervals.

(-∞, -13), (-13, 7), (7, ∞)

Take a random value in each of the above intervals and check with the inequality (x + 13)(x - 7) < 0.

When x = -14 ∈ (-∞, -13),

(-14 + 13)(-14 - 7) < 0

(-1)(-21) < 0

21 < 0 (false)

When x = 0 ∈ (-13, 7),

(0 + 13)(0 - 7) < 0

(13)(-7) < 0

-91 < 0 (true)

When x = 8 ∈ (7, ∞),

(8 + 13)(8 - 7) < 0

(21)(1) < 0

21 < 0 (false)

The inequality (x + 13)(x - 7) < 0 is satisfied only by the interval (-13, 7).

So, x ∈ (-13, 7).

-13 < x < 7

Given : x = -2c.

-13 < -2c < 7

Multiply by -1.

13 > 2c > -7

-7 < 2c < 13

Divide by 2.

-3.5 < c < 6.5

c is an integer and we have to find the largest possible value of c.

Therefore,

c = 6

Question 8 :

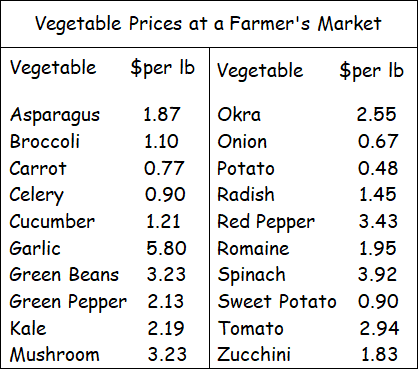
After the data were collected, the prices of five vegetables (kale, asparagus, sweet potato, okra and green beans) each went up by 20 cents per pound because they were no longer in season. Which measure(s) of central tendency would these changes affect?

(A) Mean only

(B) Median only

(C) Mean and mode only

(D) Mean, median and mode only

Answer :

Mean :

In any data, one or more values are changed, mean will also change. Since the prices of five vegetable went up by 20 cents, mean is affected.

Median :

There are twenty values in the above data.

To find the median of a data whcih contains n numbers of values, arrange the data from least to greatest (ascending order).

Then, median is ⁽ⁿ⁺¹⁾⁄₂^th value in the ascending order of the values in the data.

In the above data, there are 20 values. 

So, median ⁽²⁰⁺¹⁾⁄₂^th or 10.5^th value in the ascending order of the values in the data. Since 10.5 is the middle value between 10 and 11, median is the average of 10^th and 11^th values.

Since the median lies between 10^th and 11^th values, arrenge the values from least to greatest up to 11th value.

0.48, 0.67, 0.77, 0.90, 0.90, 1.10, 1.21, 1.45, 1.83, 1.87, 1.95

Median is the average of 1.87 and 1.95.

1.87 is the price of asparagus. Since its price went up by 20 cents, median will change.

So, median is also affected.

Mode :

In the twenty values of the given data, there are two values, eachone reapeted twice.

0.90, 0.90, 3.23, 3.23

The mode is 0.90 and 3.23.

One of the 3.23 is the price of green beans which went up by 20 cents. Then the new price of green beans is 3.43.

Now, the repeated values are

0.90, 0.90, 3.43, 3.43

(the first 3.43 is the price of green beans and the secont 3.43 is the price of red pepper)

Now, the mode is 0.90 and 3.43.

So mode is also affected.

Conslusion :

When the prices of five vegetables (kale, asparagus, sweet potato, okra and green beans) each went up by 20 cents per pound, mean, median and mode are all affected.

Therefore, option (D) is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.