REPRESENTING PROPORTIONAL RELATIONSHIPS WITH TABLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
In 1870, the French writer Jules Verne published 20,000 Leagues Under the Sea, one of the most popular science fiction novels ever written. One definition of a league is a unit of measure equaling 3 miles.
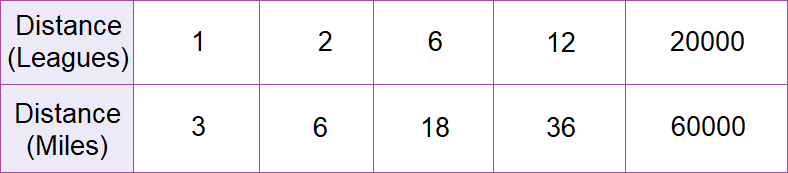
A. What relationships do you see among the numbers in the table?
Every number in the bottom row is 3 times the number in the top row.
B. For each column of the table, find the ratio of the distance in miles to the distance in leagues. Write each ratio in simplest form.
3 : 1 = 3 : 1
6 : 2 = 3 : 1
18 : 6 = 3 : 1
36 : 12 = 3 : 1
60,000 : 20,000 = 3 : 1
C. What do you notice about the ratio?
They are all equal to 3 : 1.
D. If you know the distance between two points in leagues, how can you find the distance in miles?
Multiply the distance in leagues by 3.
E. If you know the distance between two points in miles, how can you find the distance in leagues?
Divide the distance in miles by 3.
Example 2 :
The table shows the relationship between temperatures measured on the Celsius and Fahrenheit scales.

A. Is the relationship between the temperature scales proportional ? Why or why not?
No; the ratios of the numbers in each column are not equal.
B. Describe the graph of the Celsius-Fahrenheit relationship.
A line starting at (0, 32) and slanting upward to the right.
Example 3 :
The table shows the relationship between length of side of square, perimeter of square and area of square.

A. Are the length of a side of a square and the perimeter of the square related proportionally ? Why or why not?
Yes. The ratio of the perimeter of a square to its side length is always 4.
B. Are the length of a side of a square and the area of the square related proportionally ? Why or why not?
No. The ratio of the area of a square to its side length is not constant.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Specifying Units of Measure
Dec 15, 25 07:09 PM
Specifying Units of Measure -
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems