RELATIONSHIP BETWEEN SIDE LENGTHS AND ANGLES WORKSHEET

Problem 1-5 : To try to trick you, the following triangles are not drawn to scale. State the largest side of each triangle.

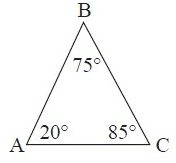
Problem 1 :

Problem 2 :

Problem 3 :

Problem 4 :

Problem 5 :

Problem 6 :

The following triangle is not drawn to scale. State the smallest side.

Answers

1. Answer :

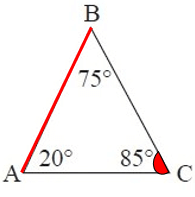
By observing the figure above,

∠C  =  85°,  it is the largest interior angle.

We know that the longest side is always opposite the largest interior angle.

So, the largest side is AB.

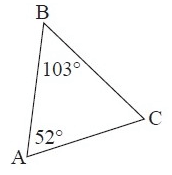
2. Answer :

By observing the figure, the measure of ∠C is not given. So we have to find ∠C.

We know that, the sum of the interior angles of a triangle is 180˚.

∠A + ∠B + ∠C  =  180°

52° + 103° + ∠C  =  180°

155°+ ∠C  =  180°

Subtract 155° from both sides.

∠C  =  25°

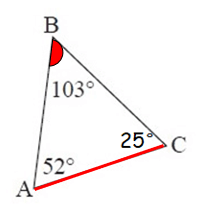
Now, both m∠A and m∠C are less than m<B.

∠B = 103°, it is the largest interior angle.

So, the largest side is AC.

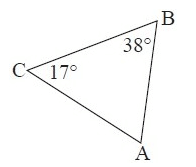
3. Answer :

By observing the figure, the measure of ∠A is not given.

To find ∠A,

∠A + ∠B + ∠C  =  180°

∠A + 38° + 17°  =  180°

∠A + 55°  =  180°

Subtract 55° from both sides.

∠A  =  125°

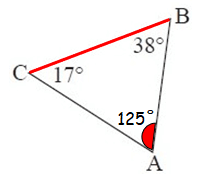
Now, both m∠B and m∠C are less than m∠A.

∠A = 125°, it is the largest interior angle.

So, the largest side is BC.

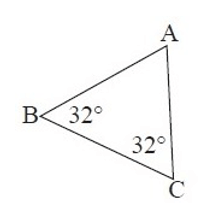
4. Answer :

By observing the figure, the measure of ∠A is not given.

To find ∠A,

∠A + ∠B + ∠C  =  180°

∠A + 32° + 32°  =  180°

∠A + 64°  =  180°

Subtract 64° from both sides.

∠A  =  116°

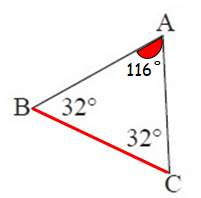
Now, both m∠B and m∠C are less than m∠A.

∠A = 116°, it is the largest interior angle.

So, the largest side is BC.

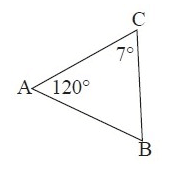
5. Answer :

By observing the figure, the measure of ∠B is not given.

To find ∠B,

∠A + ∠B + ∠C  =  180°

120˚ + ∠B + 7˚  =  180˚

∠B + 127°  =  180°

Subtract 127° from both sides.

∠B  =  53°

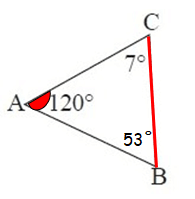
Now, both m∠B and m∠C are less than m∠A.

∠A = 120°, it is the largest interior angle.

So, the largest side is BC.

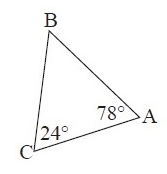
6. Answer :

By observing the figure, the measure of ∠B is not given.

To find ∠B,

∠A + ∠B + ∠C  =  180°

78° + ∠B + 24°  =  180°

∠B + 102°  =  180°

Subtract 102° from both sides.

∠B  =  78°

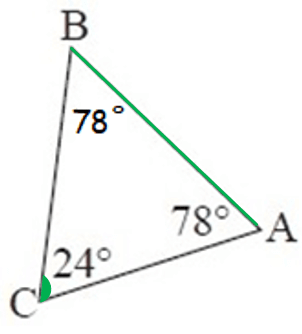
The smallest angle is ∠C, the side which is opposite to smaller angle is AB. So, the smallest side is AB.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.