APPLICATION PROBLEMS ON RATE OF CHANGE
Problem 1 :
Two sides of a triangle are 4 m and 5 m in length and the angle between them is increasing at the rate of 0.06 rad/sec. Find the rate at which the area of the triangle is increasing when the angle between the sides of fixed length is π/3.
Solution :
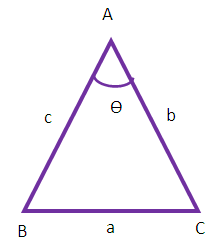
Let b and h be the base and height of the triangle ABC.
Let θ radian be the angle between the sides AB and AC when b = 5 cm, c = 4 cm
dθ/dt = 0.06 radian/sec.
Let A and t be the area of the triangle and time taken respectively.
Find the value of dA/dt when θ = π/3
Area of triangle ABC = (1/2) b c sin θ
dA/dt = (1/2) b c cos θ (dθ/dt)
= (1/2) (5) (4) (sin π/3) (0.06)
= (1/2) (20) (1/2) (0.06)
= (20/4) (0.06)
= 0.3 m²/sec
Therefore, the area is increasing at the rate of 0.03 m2/sec.
Problem 2 :
Two sides of a triangle have length 12 m and 15 m. The angle between them is increasing at a rate of 2°/min. How fast is the length of third side increasing when the angle between the sides of fixed length is 60° ?
Solution :
Let ABC be the given triangle
Length of the side AB = 12 m
length of the sides BC = 15 m
Let θ be the angle between the sides AB and BC at "t" minutes
dθ/dt = 2°(π/180)'
dθ/dt = π/90
now we have to find db/dt when θ = 60°
b2 = c2 + a2 - 2 a c cos θ
2 b (db/dθ) = 0 + 0 - 2 a c (-sin θ) (dθ/dt)
2 b (db/dθ) = 2 a c (sin θ) (dθ/dt)
b (db/dθ) = a c (sin θ) (dθ/dt) --- (1)
now apply a = 15, c = 12 and θ = 60°
b2 = 122 + 152 - 2 (15) (12) cos 60°
b2 = 144 + 225 - 360 (1/2)
b2 = 369 - 180
b2 = 189
b = √189
now let us apply these values in the first equation
b (db/dθ) = a c (sin θ) (dθ/dt) --- (1)
√189 (db/dθ) = 15 ⋅ 12 (sin 60°) (π/90)
db/dθ = 15 ⋅ 12 ⋅ (√3/2) (π/90)/√189
db/dθ = [(180) (√3) (π)]/[2 (√189) (90)]
(db/dθ) = π/√63 m/minutes
Therefore, the rate of change of the third side is π/√63 m/minutes.
Problem 3 :
Gravel is being dumped from a conveyor belt at a rate of 30 ft³/min and its coarsened such that it forms a pile in the shape of cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 10 ft high?
Solution :
Let V = the volume of the cone, t = time, r = radius and h = height of the cone.
Here we have a information that the base diameter and height are always equal.
So, 2r = h
Rate of change of volume (dV/dt) = 30
Now, we have to find how fast is the height of the pile increasing when the pile is 10 ft.
h = 10
Volume of cone V = (1/3) π r² h
V = (1/3) π (h/2)² h
V = (1/3) π (h³/4)
dV/dt = (1/3) π (3 h²/4) (dh/dt)
Apply, h = 10 and dV/dt = 30
30 = (1/3) π [3 (10)²/4] (dh/dt)
(30 x 3 x 4)/300 π = (dh/dt)
6/5π = dh/dt
dh/dt = (6/5 π) ft/min
Therefore, the height is increasing at the rate of (6/5π) ft/min
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Sum of the Three Angles of a Triangle
Apr 26, 24 09:20 PM
Sum of the Three Angles of a Triangle - Concept - Solved Examples -
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems