SUM OF THE THREE ANGLES OF A TRIANGLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In a triangle,
sum of the three angles = 180°
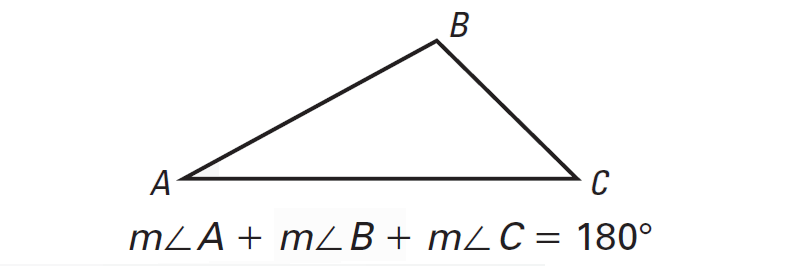
If the sum of the three angles is not equal to 180°, then we can conclude that the three angles can not be the angles of a triangle.
Example 1 :
Can 30°, 60° and 90° be the angles of a triangle?
Solution :
Add the given ngle measrues :
30° + 60° + 90° = 180°
Since the given angle measures 30°, 60° and 90° add up to 180°, they can be the angles of a triangle.
Example 2 :
Can 35°, 55° and 95° be the angles of a triangle?
Solution :
Add the given ngle measrues :
35° + 55° + 95° = 185° ≠ 180°
Since the given angle measures do not add up to 180°, they can not be the angles of a triangle.
Example 3 :
In the triangle shown below, what is the value of x?
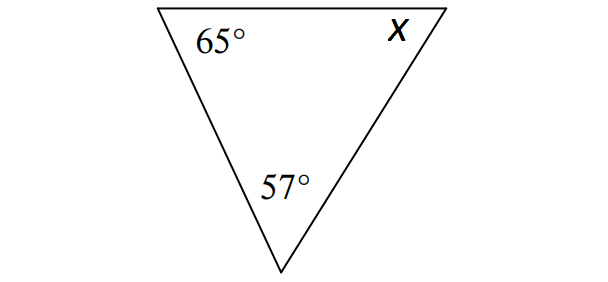
Solution :
In the triangle shown above,
x + 65° + 57° = 180°
x + 122° = 180°
Subtract 122° from both sides.
x = 58°
Example 4 :
In the triangle shown below, what is the value of y?
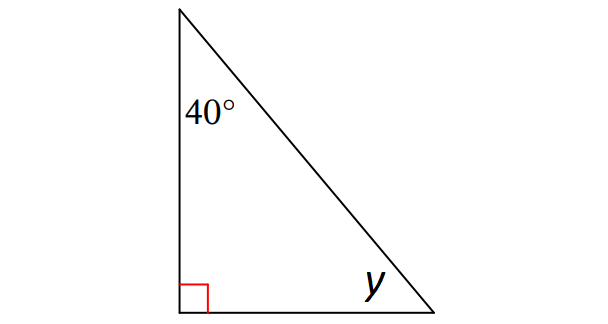
Solution :
In the triangle shown above,
y + 90° + 40° = 180°
y + 130° = 180°
Subtract 130° from both sides.
y = 50°
Example 5 :
In the triangle shown below, what is the value of k?
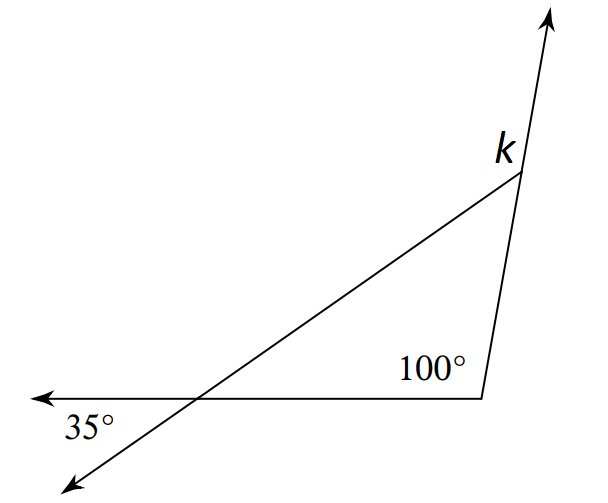
Solution :
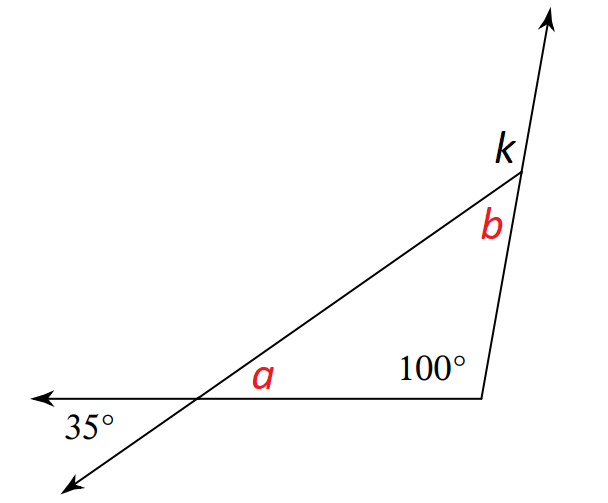
In the triangle shown above, a and 35° are vertical angles and they are equal.
a = 35°
sum of the angles in a triangle = 180°
a + b + 100° = 180°
Substitute a = 35°.
35° + b + 100° = 180°
b + 135° = 180°
Subtract 135° from both sides.
b = 45°
b and k are linear pair.
b + k = 180°
Substitute b = 45°.
45° + k = 180°
Subtract 45° from both sides.
k = 135°
Example 6 :
In an isosceles triangle, the measure of each of the two congruent angles is equal to 2.5 times the measure of the third angle. Find the the angles of the isosceles triangle.
Solution :
Let x be the measure of the third angle.
Then, the measure of each of the two congruent angles :
= 2.5x
The three angles of the isosceles triangle are 2.5x, 2.5x and x.
sum of the angles of a triangle = 180°
2.5x + 2.5x + x = 180°
6x = 180°
Divide both sides by 6.
x = 30°
2.5x = 2.5(30°) = 75°
The measures of angles of the triangle are 75°, 75° and 30°.
Example 7 :
The angles of a triangle are in the ratio 11 : 13 : 12. Find the measures of angles of the triangle.
Solution :
It is given that he triangle are in the ratio
11 : 13 : 12
To get the measure of each angle from the ratio, multiply eac term of the ratio by the same number, say k.
The three angles of the triangle are
11x, 13x and 12x
sum of the angles of a triangle = 180°
11x + 13x + 12x = 180°
36x = 180°
Divide both sides by 36.
x = 5°
First angle :
= 11x
= 11(5°)
= 55°
Second angle :
= 13x
= 13(5°)
= 65°
Third angle :
= 12x
= 12(5°)
= 60°
The measures of angles of the triangle are 55°, 65° and 60°.
Example 8 :
The measure of first angle of a triangle is 50% more than the measure of second angle and the measure of third angle is 28° less than the measure of first angle. Find the measures of three angles of the triangle.
Solution :
Let x be the measure of second angle.
Then the measure of first angle :
= (100 + 50)% of x
= 150% of x
= 1.5x ----(1)
It is given that the measure of the third angle is 28° less than the first angle.
The measure of third angle :
= 1.5x - 28° ----(2)
The three angles of the triangle are
1.5x, x and (1.5x - 28°)
sum of the angles of a triangle = 180°
1.5x + x + (1.5x - 28°) = 180°
1.5x + x + 1.5x - 28° = 180°
4x - 28° = 180°
Add 28° to both sides.
4x = 208°
Divide both sides by 4.
x = 52°
second angle = 52°
To know the measures of first and third angles, substitute x = 52° in (1) and (2).
First angle :
= 1.5(52°)
= 78°
Third angle :
= 1.5(52°) - 28°
= 78° - 28°
= 50°
The measures of angles of the triangle are 78°, 52° and 50°.
Example 9 :
The angles measures of a triangle are three consecutive even integers. Find the measures of angles of the triangle.
Solution :
Since the angles of a triangle are three consecutive even integers, the angles can be assumed as
x, (x + 2) and (x + 4)
sum of the angles of a triangle = 180°
x + (x + 2) + (x + 4) = 180
x + x + 2 + x + 4 = 180
3x + 6 = 180
Subtract 6 from both sides.
3x = 174
Divide both sides by 3.
x = 58
x + 2 = 58 + 2 = 60
x + 4 = 58 + 4 = 62
The measures of angles of the triangle are 58°, 60° and 62°.
Example 10 :
In a triangle, if the second angle is 2 times the first angle and the third angle is 3 times the first angle, find the measures of angles of the triangle.
Solution :
Let x be the first angle.
Then the measure of second angle = 2x.
The measure of third angle = 3x.
sum of the angles of a triangle = 180°
x + 2x + 3x = 180°
6x = 180°
Divide both sides by 6.
x = 30°
2x = 2(30°) = 60°
3x = 3(30°) = 90°
The measures of angles of the triangle are 30°, 60° and 90°.
Example 11 :
There is an argument between Kevin and Peterson. Kevin says that a triangle can have two right angles. But, Peterson refuses Kevin's above staement. Is Kevin's staement correct? Explain.
Solution :
Sum of the two right angles :
= 90° + 90°
= 180°
When a triangle has two right angles, after the third angle is included, the sum of the three angles of the triangle will be greater than 180°, which contradicts the fact that the sum of the three angles of a triangle is equal to 180°.
So, Kevin's statement is INCORRECT.
Example 12 :
"A traingle can have two obtuse angles"
Is the above statement corect? Explain.
Solution :
Obtuse angle > 90°
Since the measure of an obtuse angle is greater than 90°, sum of the two obtuse angles must be greater than 180°.
When a triangle has two obtuse angles, after the third angle is included, the sum of the three angles of the triangle will still be greater than 180°, which contradicts the fact that the sum of the three angles of a triangle is equal to 180°.
So, the given statemtn is INCORRECT.
Example 13 :
"A traingle can have two acute angles"
Is the above statement corect? Explain.
Solution :
Acute angle < 90°
Since the measure of an acute angle is less than 90°, sum of the two acute angles must be less than 180°.
When a triangle has two acute angles, a third angle can be included such that the sum of the three angles of the triangle is equal to 180°.
So, the given statement is CORRECT.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
