RATE OF CHANGE AND INITIAL VALUE WORKSHEET

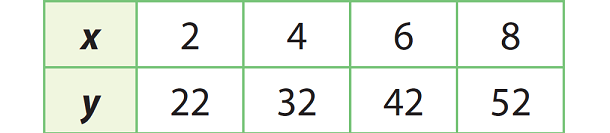
Problem 1 :

Find the slope and y-intercept of the line represented by the table. And also find the equation of the line in slope-intercept form.

Problem 2 :

A phone salesperson is paid a minimum weekly salary and a commission for each phone sold, as shown below. Confirm that the relationship is linear and give the constant rate of change and the initial value.

Answers

1. Answer :

Step 1 :

Confirm that the rate of change is constant.

Change in y-value / change in x-value :

=  (32 - 22)/(4 - 2)  =  10/2  =  5

=  (42 - 32)/(6 - 4)  =  10/2  =  5

=  (52 - 42)/(8 - 6)  =  10/2  =  5

The rate of change is a constant and it is 5.

So, the slope is 5.

Step 2 :

Find the initial value y. That is, the value of y when x = 0. 

Work backward from x = 2 to x = 0 to find the initial value.

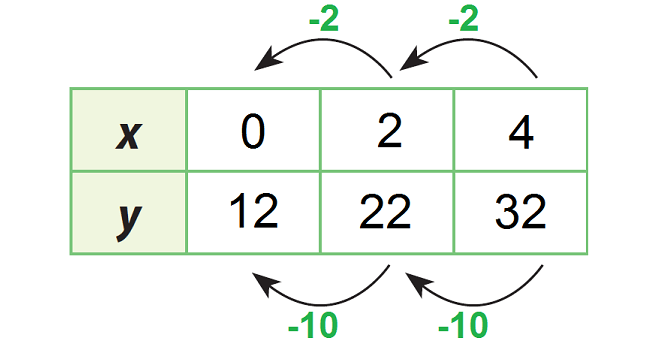
The initial value is 12. That is, y-intercept is 12. 

So, the equation of the line is  y = 5x + 12.

2. Answer :

Step 1 : 

Confirm that the rate of change is constant.

Phones sold (10 to 20) :

Change in income/Change in phones sold is

=  (630 - 480)/(20 - 10)

=  150/10

=  15

Phones sold (20 to 30) :

Change in income/Change in phones sold is

=  (780 - 630)/(30 - 20)

=  150/10

=  15

Phones sold (30 to 40) :

Change in income/Change in phones sold is

=  (930 - 780)/(40 - 30)

=  150/10

=  15

The rate of change is a constant and it is 15.

The salesperson receives a $15 commission for each phone sold.

Step 2 :

Find the initial value when the number of phones sold is 0.

Work backward from x = 10 to x = 0 to find the initial value.

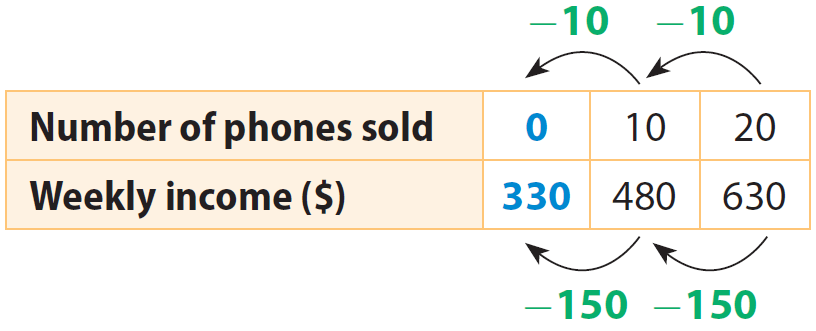
The initial value is $330. The salesperson receives a salary of $330 each week before commissions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.