PROVING TRIANGLES ARE CONGRUENT

Triangle Congruence Postulates and Theorems

1. Side-Side-Side (SSS) Congruence Postulate

If three sides of one triangle is congruent to three sides of another triangle, then the two triangles are congruent.

2. Side-Angle-Side (SAS) Congruence Postulate

If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.

3. Angle-Side-Angle (ASA) Congruence Postulate

If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.

4. Angle-Angle-Side (AAS) Congruence Postulate

If two angles and non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.

5. Hypotenuse-Leg (HL) Theorem

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

6. Leg-Acute (LA) Angle Theorem

If a leg and an acute angle of one right triangle are congruent to the corresponding parts of another right triangle, then the two right triangles are congruent.

7. Hypotenuse-Acute (HA) Angle Theorem

If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent.

8. Leg-Leg (LL) Theorem

If the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.

Caution :

SSA and AAA can not be used to test congruent triangles.

Solving Problems Using Triangle Congruence Postulates and Theorems

Problem 1 :

In the diagram given below, prove that ΔPQW ≅ ΔTSW. 

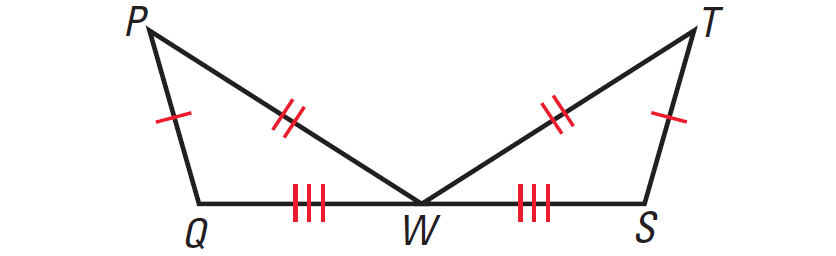
Solution :

Problem 2 :

In the diagram given below, prove that ΔABC  ≅  ΔFGH. 

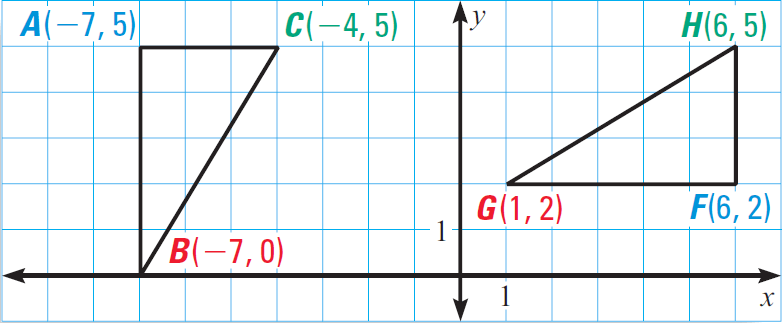
Solution :

Because AB = 5 in triangle ABC and FG = 5 in triangle FGH, 

AB  ≅  FG.

Because AC = 3 in triangle ABC and FH = 3 in triangle FGH, 

AC  ≅  FH.

Use the distance formula to find the lengths of BC and GH. 

Length of BC : 

BC  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  B(-7, 0) and (x₂, y₂)  =  C(-4, 5)

BC  =  √[(-4 + 7)² + (5 - 0)²]

BC  =  √[3² + 5²]

BC  =  √[9 + 25]

BC  =  √34

Length of GH : 

GH  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  G(1, 2) and (x₂, y₂)  =  H(6, 5)

GH  =  √[(6 - 1)² + (5 - 2)²]

GH  =  √[5² + 3²]

GH  =  √[25 + 9]

GH  =  √34

Conclusion :

Because BC = √34 and GH = √34,

BC  ≅  GH

All the three pairs of corresponding sides are congruent. By SSS congruence postulate, 

ΔABC  ≅  ΔFGH

Problem 3 :

In the diagram given below, prove that ΔAEB  ≅  ΔDEC. 

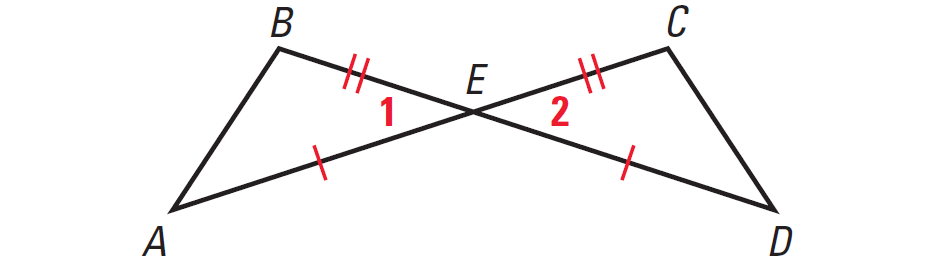
Solution :

Problem 4 :

In the diagram given below, prove that ΔABD ≅ ΔEBC. 

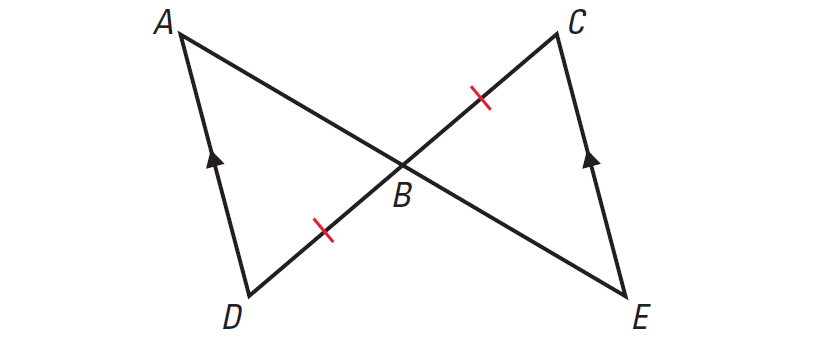
Solution :

Problem 5 :

In the diagram given below, prove that ΔEFG  ≅  ΔJHG. 

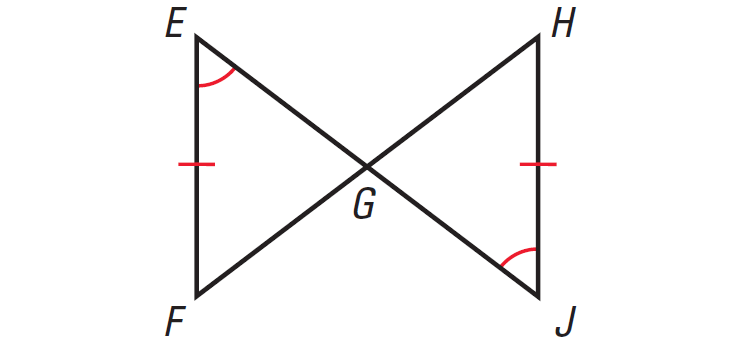
Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.