PROVING LINES ARE PARALLEL

Let us recall the definition of parallel lines, meaning they are a pair of lines that never intersect and are always the same distance apart. Then we think about the importance of the transversal, the line that cuts across two other lines. At this point, we link the railroad tracks to the parallel lines and the road with the transversal. Now what ?

Now we get to look at the angles that are formed by the transversal with the parallel lines. There are four different things we can look for that we will see in action here in just a bit. Just remember that when it comes to proving two lines are parallel, all we have to look at are the angles. Specifically, we want to look for pairs of :

(i) Corresponding angles

(ii) Alternate interior angles

(iii) Alternate exterior angles, or

(iv) Supplementary angles

Corresponding Angles Converse

If two lines are cut by a transversal so that corresponding angles are congruent, then the lines are parallel.

The diagram given below illustrates this.

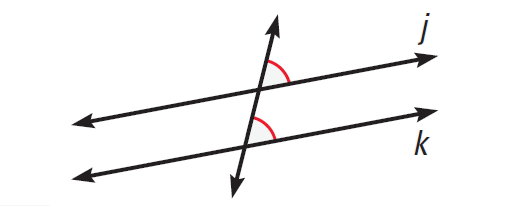
In the diagram above, j||k.

Alternate Interior Angles Converse

If two lines are cut by a transversal so that alternate interior angles are congruent, then the lines are parallel.

The diagram given below illustrates this.

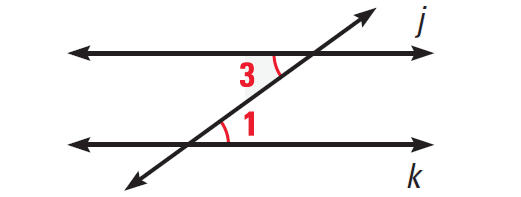
In the diagram above, if ∠1 ≅ ∠3, then j||k.

Consecutive Interior Angles Converse

If two lines are cut by a transversal so that consecutive interior angles are supplementary, then the lines are parallel.

The diagram given below illustrates this.

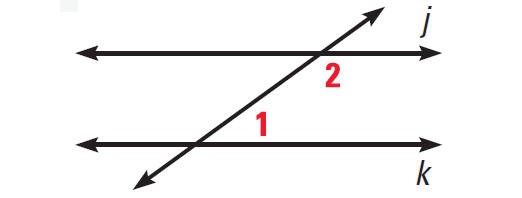
In the diagram above, if ∠1 + ∠2 = 180°, then j||k.

Alternate Interior Angles Converse

If two lines are cut by a transversal so that alternate exterior angles are congruent, then the lines are parallel.

The diagram given below illustrates this.

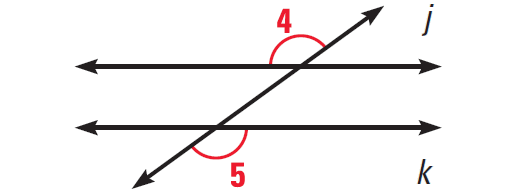
In the diagram above, if ∠4 ≅ ∠5, then j||k.

Problem 1 :

In the diagram given below, if ∠1 ≅ ∠2, then prove m||n.

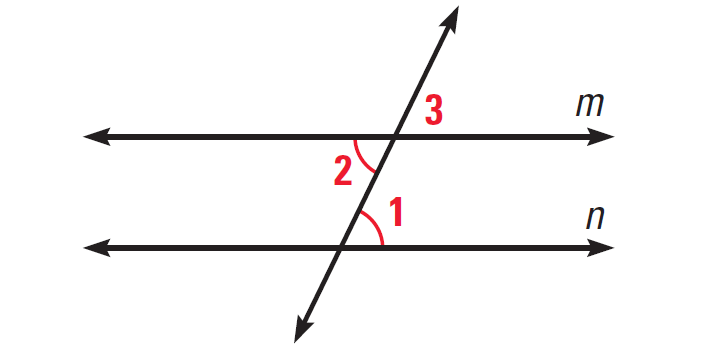
Solution :

Problem 2 :

In the diagram given below, if ∠4 and ∠5 are supplementary, then prove g||h.

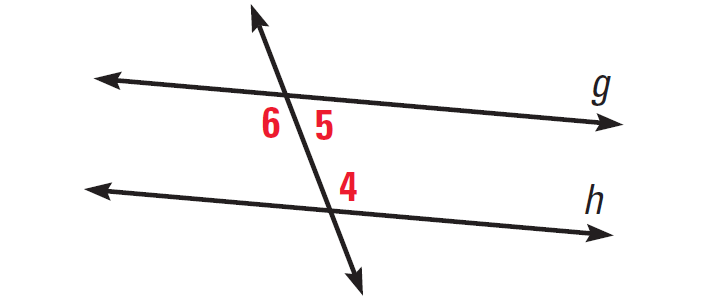
Solution :

We are given that ∠4 and ∠5 are supplementary. By the linear pair postulate, ∠5 and ∠6 are also supplementary, because they form a linear pair. By the congruence supplements theorem, it follows that ∠4 ≅ ∠6. Therefore, by the alternate interior angles converse, g and h are parallel.

Problem 3 :

In the diagram given below, find the value of x that makes j||k.

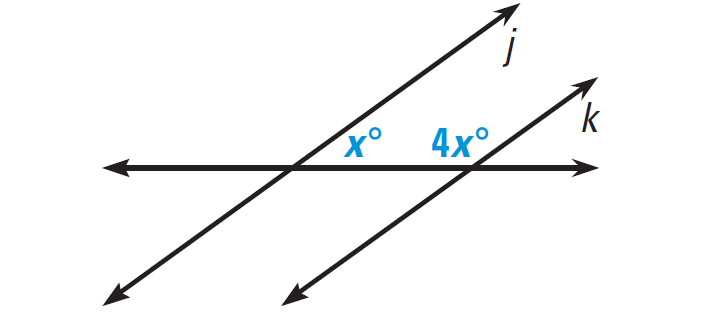
Solution :

Lines j and k will be parallel if the marked angles are supplementary.

x° + 4x° = 180°

5x = 180

x = 36

So, x = 36 makes j||k.

Problem 4 :

If two boats sail at a 45° angle to the wind as shown, and the wind is constant, will their paths ever cross ? Explain.

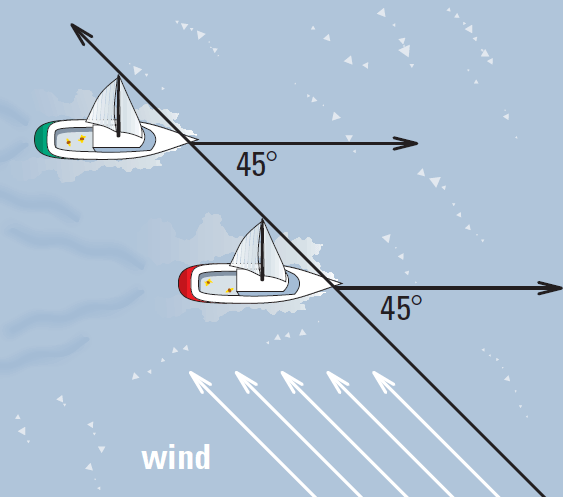
Solution :

Because corresponding angles are congruent, the paths of the boats are parallel. Parallel lines do not intersect. So the paths of the boats will never cross.

Problem 5 :

In the diagram given below, decide which rays are parallel. 

(i) Is EB parallel to HD?

(ii) Is EA parallel to HC?

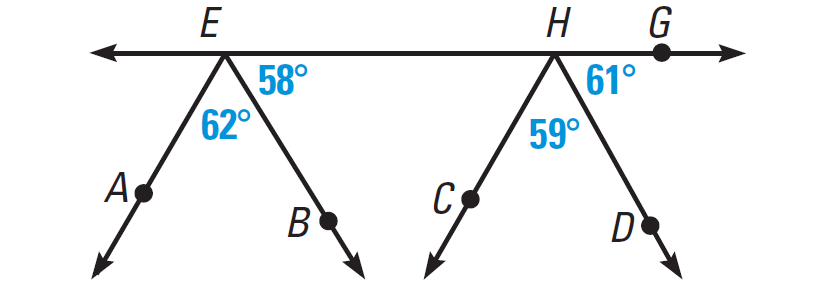
Solution (i) :

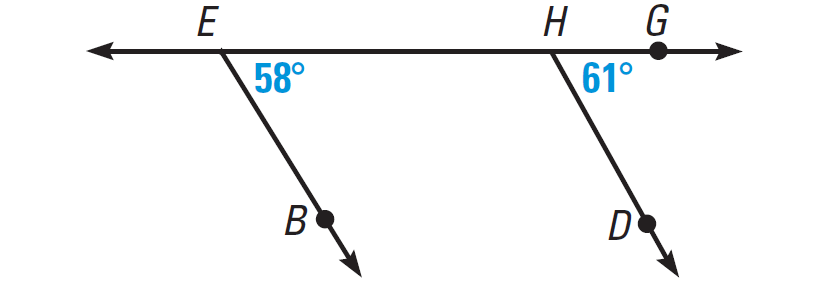
m∠BEH = 58°

m∠DHG = 61° 

∠BEH and ∠DHG are corresponding angles, but they are not congruent. So EB and HD are not parallel.

Solution (ii) :

m∠AEH = 62° + 58° = 120°

m∠CHG = 59° + 61° = 120°

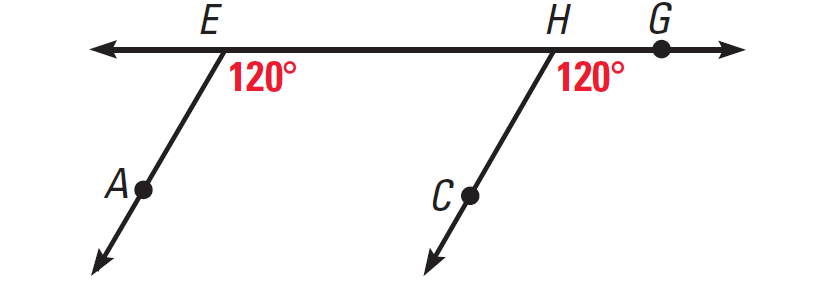
∠AEH and ∠CHG are congruent corresponding angles. So AE and CH are parallel.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.