SOLVING WORD PROBLEMS ON PROPORTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A proportion is an equation that states that two ratios or rates are equivalent.
Examples :
⅓ and ²⁄₆ are equivalent ratios
⅓ = ²⁄₆ is a proportion
We use cross product rule in proportion to solve many real world problems.
Let us consider the proportion
a : b = c : d
To know the cross product rule, first we have to know about extremes and means.
It has been explained in the picture given below.
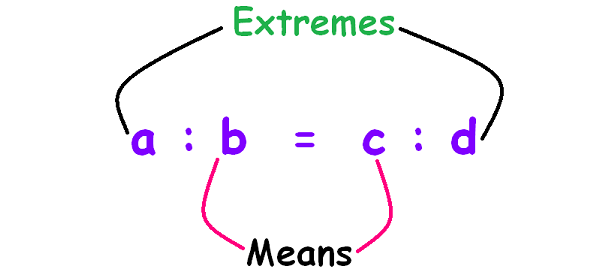
Cross Product Rule :
Product of extremes = Product of means
ad = bc
Problem 1 :
Christina takes 2 hours to travel 35 km. How far will she travel in 6 hours ?
Solution :
The ratio between number of hours and distance traveled is
2 : 35 ----(1)
Let x be the distance traveled by her in 6 hours.
6 : x ----(2)
From (1) and (2),
2 : 35 = 6 : x
2 ⋅ x = 6 ⋅ 35
2x = 210
Divide each side by 2.
x = 105
So, the distance covered by Christina in 6 hours is 105 km.
Problem 2 :
If a person reads 20 pages in a book in 2 hours, how many pages will he read in 8 hours at the same speed ?
Solution :
The ratio between number of pages and time taken
= 20 : 2
= 10 : 1 ----(1)
Let x be the number of pages read in 8 hours.
x : 8 ----(2)
From (1) and (2),
10 : 1 = x : 8
10 ⋅ 8 = 1 ⋅ x
80 = x
So, the person can read 80 pages in 8 hours.
Problem 3 :
If 15 people can repair a road of length 150 meters, at the same rate, how many people are needed to repair a road of length 420 meters.
Solution :
The ratio between number of people and length of road repaired is
= 15 : 150
= 1 : 10 ----(1)
Let x be the number of people needed to repair a road of length 420 meters.
x : 420 ----(2)
From (1) and (2),
1 : 10 = x : 420
1 ⋅ 420 = 10 ⋅ x
420 = 10x
Divide each side by 10.
42 = x
So, 42 people are needed to repair a road of length 420 meters.
Problem 4 :
If the cost of 10 kg rice is $400, then find the cost of 3 kg rice.
Solution :
The ratio between the number of kilograms of rice and the cost is
10 : 400 ----(1)
Let x be the cost of 3 kilograms of rice.
3 : x ----(2)
From (1) and (2),
10 : 400 = 3 : x
10 ⋅ x = 3 ⋅ 400
10x = 1200
Divide each side by 10.
x = 120
So, the cost of 3 kg rice is $120.
Problem 5 :
A car needs 12 liters of petrol to cover a distance of 156 miles. How much petrol will be required for the car to cover a distance of 1300 miles?
Solution :
The ratio between the number of liters of petrol and distance covered is
= 12 : 156
= 1 : 13 ----(1)
Let x be the number of liters of petrol required to cover a distance 1300 km.
x : 1300 ----(2)
From (1) and (2),
1 : 13 = x : 1300
1(1300) = x(13)
1300 = 13x
Divide each side by 13.
100 = x
So, 100 liters of petrol will be required to cover a distance of of 1300 miles.
Problem 6 :
If you can buy one can of pineapple chunks for $2 then how many can you buy with $10?
Solution :

From the given information, number of cans of pineapple chunks and the cost are in the ratio
1 : 2
Let x be the number of cans that we buy.
Then,
1 : 2 = x : 10
1 ⋅ 10 = 2 ⋅ x
10 = 2x
10 = 2x
5 = x
So, we can buy 5 apples with $10.
Problem 7 :
Shawna reduced the size of a rectangle to a height of 2 in. What is the new width, if it was originally 24 in wide and 12 in tall?
Solution :
From the given information, the width and height of the rectangle are in the ratio
24 : 12 = 2 : 1
Because the original width and height of the rectangle are in the ratio 2 : 1, the width and height of he resized rectangle will also be in the same ratio.
And also, the height of the rectangle is reduced to 2 inches.
Let x be the width of the resized rectangle.
Then,
2 : 1 = x : 2
2 ⋅ 2 = 1 ⋅ x
4 = x
So, the width of the resized rectangle is 4 inches.
Problem 8 :
One cantaloupe costs $2. How many cantaloupes can we buy for $6?
Solution :

From the given information, number of cans of pineapple chunks and the cost are in the ratio
1 : 2
Let x be the number of cantaloupe that we buy.
Then,
1 : 2 = x : 6
1 ⋅ 6 = 2 ⋅ x
6 = 2x
3 = x
So, we can buy 3 cantaloupes for $6.
Problem 9 :
Ming was planning a trip to Western Samoa. Before going, she did some research and learned that the exchange rate is 6 Tala for $2. How many Tala would she get if she exchanged $6?
Solution :
From the given information, the exchange rate of Tala and Dollar are in the ratio
6 : 2 = 3 : 1
Let x be the number of Tala that Ming would expect.
Then,
3 : 1 = x : 6
3 ⋅ 6 = 1 ⋅ x
18 = x
So, Ming would get 18 Tala, if she exchanged $6.
Problem 10 :
Jasmine bought 32 kiwi fruit for $16. How many kiwi she Lisa buy, if she has $4?
Solution :
From the given information, we come to know that number of kiwi fruits to the cost is in the ratio.
32 : 16 = 2 : 1
Let x be the number of kiwi that jasmine buy for $4.
2 : 1 = x : 4
2 ⋅ 4 = 1 ⋅ x
8 = x
So, Jasmine can buy 8 kiwi fruits for $4.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

