PROBLEMS ON VOLUME OF CONE

Problem 1 :

A right angled triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the fixed side of 12 cm. Find the volume of the solid generated.

Solution :

In any right triangle the longer side must be hypotenuse side. The longer side of the given sides is 13 cm.

So it must be hypotenuse side of the triangle.

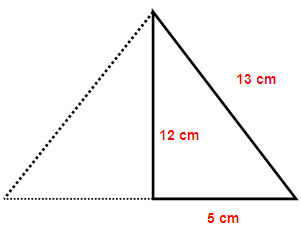
From the diagram we know that slant height is 13 cm, radius is 5 cm and height is 12 cm.

l  =  13 cm, r  =  5 cm and h = 12 cm

Volume of cone   =   (1/3)Πr²h

=  (1/3) ⋅ (22/7) ⋅ 5²⋅12

=  (22/7) ⋅ 5 ⋅ 5 ⋅ 4

=  314.29 cm³

Volume of cone  =  314.29 cm³

Problem 2 :

The radius and height of a right circular cone are in the ratio 2:3. Find the slant height if its volume is 100.48 cu.cm (take Π = 3.14)

Solution :

Radius and height of right circular cone are in the ratio

2 : 3

                                    r : h  =  2 : 3

                                    r/h  =  2/3

                                       r  =  2h/3

Volume of cone  =  100.48 cu.cm

(1/3)Πr² h  =  100.48

(1/3) (3.14) (2h/3)² h  =  100.48

(1/3) (3.14) (4h²/9) h  =  100.48

h³ = 100.48 ⋅ (3/1) ⋅ (1/3.14) ⋅ (9/4)

h³ = 8 ⋅ 27

h  =  6 cm

r  =  4 cm 

l²  =  r²+h²

l²  =  4²+6²

l  =  √52

l  =  2√13 cm

So, slant height of the cone is 2√13 cm.

Problem 3 :

The volume of a cone with circular base is 216 Π cu.cm. If the base radius is 9 cm, then find the height of the cone.

Solution :

Volume of the cone  =  216Π cu.cm

Radius of the cone  =  9 cm

(1/3) Π r² h  =  216Π

9² h  =  216 ⋅ 3

h  =  216 ⋅ 3 ⋅ (1/9) (1/9)

h  =  24/3

h  =  8 cm

Required height of cone is 8 cm.

Problem 4 :

A solid cone is made from a material which has a density of 8.7 g/cm³. The dimensions of the cone are shown below. Find the mass of the cone.

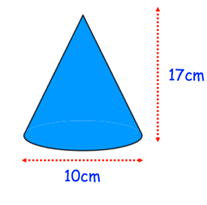
Solution :

Mass = Volume x density

Volume of cone = (1/3) Π r² h 

Radius (r) = 10/2 ==> 5 cm

Height (h) = 17 cm

= (1/3) x 3.14 x (5)² x (17)

= 1334.5/3

= 444.8

Approximately 445 cm³

Mass = 445 x 8.7

= 3871.5

So, the mass of the cone is 3871.5.

Problem 5 :

The sphere and cone have an equal volume. Find the radius of the sphere.

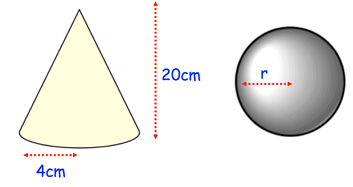
Solution :

Volume of cone = Volume of sphere

(1/3) Π r² h = (4/3) Π r³

Π r² h = 4 Π r³

4² x 20 = 4 r³

r³ = 4 x 20

r = ∛(4 x 20)

r = 2 ∛10

So, the radius of the sphere is 2∛10 cm.

Problem 6 :

The inside of each glass is shaped like a cone. Which glass can hold more liquid? How much more?

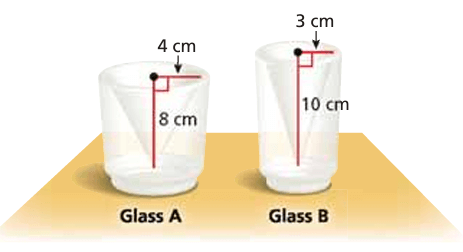
Solution :

By finding the capacity of each glass, we may find in which glass we have more quantity of liquid.

Quantity of liquid in glass A :

= (1/3) Π r² h

= (1/3) Π 4² (8)

= 133.97 cm³

Quantity of liquid in glass B :

= (1/3) Π r² h

= (1/3) Π 3² (10)

= 94.2 cm³

So, glass A will contain more capacity of liquid.

Problem 7 :

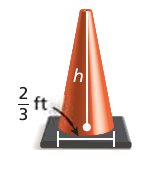
Find the height of the cone. Round your answer to the nearest tenth

Volume of the cone = (1/18)Π ft³

Solution :

(1/3) Π r² h = (1/18)Π ft³

r = 2/3 ft and h = ?

(1/3) (2/3)² h = (1/18)

h = (1/18) x (3/1) x (9/4)

h = 3/8 ft

So, the required height is 3/8 ft.

Problem 8 :

Midori had a cone full of birdseed to feed the birds at the park. What is the volume of the birdseed of the cone ?

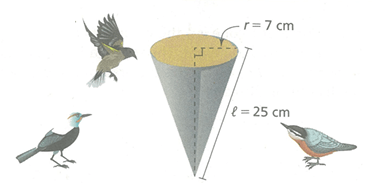
Solution :

radius = 7 cm, slant height = 25 cm

Since we have birdseed full of cone, by finding the capacity of the cone we find the volume of birdseed in the cone.

We may find height of the cone using Pythagorean theorem,

l² = r² + h²

h = √l² - r²

h = √25² - 7²

= √(625 - 49)

= √576

= 24

So, the required height is 24 cm. By applying these values in the formula, we get

= (1/3) Π r² h

= (1/3) x 3.14 x (7)² x 24

= (1/3) x 3692.64

= 1230.88 cm³

So, the required volume is 1230.88 cm³

Problem 9 :

The circumference of the base of the cone is 6Π inches, what is the volume of the cone in terms of Π ?

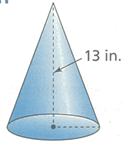
Solution :

Circumference of the base of cone = 6Π

2Πr = 6Π

r = 3 cm

Volume of cone = (1/3) Π r² h

= (1/3) Π 3² (13)

= 39Π

Volume of the cone is 39Π.

Problem 10 :

Volume of the cone is 462 cubic yards. What is the radius of the cone.

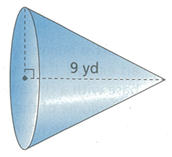
Volume of cone = 462 cubic yards

 (1/3) Π r² (9) = 462

(1/3) x 3.14 x 9 x r² = 462

r² = (462 x 3)/ (3.14 x 9)

r² = 49

r = 7 yards

So, the radius is 7 yards.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.