PROBLEMS ON FINDING VOLUME OF PYRAMID

What is volume ?

Volume is the number of three-dimensional spaces an object occupies.

It is measured in cubic units such as cubic meters, cubic centimeters, etc.

What is the volume of prisms ?

A prism is solid with a uniform cross-section. This means that no matter where it is sliced along its length, the cross-section is the same size and shape.

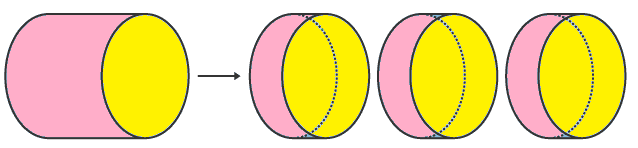
To find the volume for any solid of uniform cross-section 

Volume  =  area of cross-section × length

Find the volume of the following :

Problem 1 :

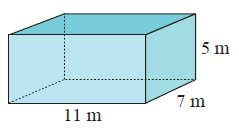
Solution :

By observing the figure, it is a rectangular prism.

Here area of cross-section is the shape of the rectangle.

To find the volume,

Volume = length × width × height

we have,

length = 11 m, width = 7 m and height = 5 m

Volume = 11 × 7 × 5

Volume = 385 m³

Problem 2 :

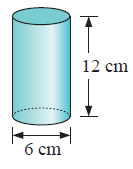
Solution :

By observing the figure, it is a cylinder.

Here area of cross-section is the shape of the circle.

To find the volume,

Volume  =  area of cross-section × length

Volume  =  area of the circle × length

Volume  =  (πr²) × h

we have,

diameter  =  6 cm,

radius (r)  =  6/2  =  3 cm and height (h)  =  12 cm  

= π(3)² × 12

= (3.14 × 9 × 12)

Volume = 339 cm³

Problem 3 :

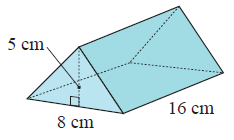
Solution :

By observing the figure, it is a triangular prism.

Here area of cross-section is the shape of the triangle.

To find the volume,

Volume  =  area of cross-section × length

Volume  =  area of the triangle × length

=  (1/2 × b ×  h) × l

we have,

base (b)  =  8 cm, height (h) = 5 cm and length (l) = 16 cm

=  1/2 × 8 × 5 × 16

Volume = 320 cm³

Problem 4 :

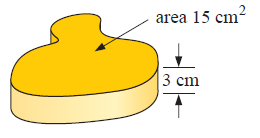
Solution :

By observing the figure, it is a irregular prism.

Here area of cross-section is the irregular shape.

To find the volume,

Volume  =  area of cross-section × length

we have,

area = 15 cm², and length = 3 cm

Volume  =  15 × 3

Volume = 45 cm³

Problem 5 :

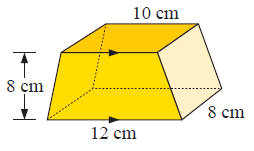
Solution :

By observing the figure, it is a trapezium prism.

Here area of cross-section is the shape of the trapezium.

To find the volume,

Volume  =  area of cross-section × length

Volume  =  area of the trapezium × length

=  1/2 × h × (b₁ + b₂) × length

we have,

base (b₁) = 12 cm, base (b₂) = 10 cm, height (h) = 8 cm and length  =  8 cm

=  1/2 × 8 × (12 + 10) × 8

= 88 × 8

Volume = 704 cm³

Problem 6 :

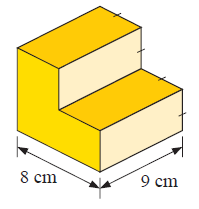
Solution :

By observing the figure, it is a irregular prism.

Here area of cross-section is the shape of the rectangle and square.

To find the volume,

Volume  =  area of cross-section × length

Volume  =  (area of the rectangle + area of the square)  × length

=  [(s²) + (l × w)] × length

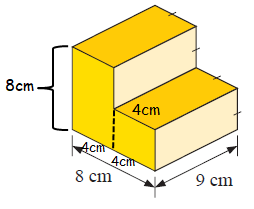
we have,

side (s) = 4 cm, length (l) = 8 cm, width (w) = 4 cm and length  =  9 cm

Volume  =  [(4²) + (8 × 4)] × 9

=  (16 + 32) × 9

Volume =  432 cm³

Problem 7 :

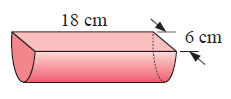
Solution :

By observing the figure, it is a semicircle prism.

Here area of cross-section is the shape of the semicircle.

To find the volume,

Volume  =  area of cross-section × length

Volume  =  area of the semicircle  × length

=  1/2 πr² × length

we have,

diameter  =  6 cm,

radius (r)  =  6/2  =  3 cm and length (l)  =  18 cm  

= 1/2π(3)² × 18

= (1/2 × 3.14 × 9) × 18

= 14.13 × 18

Volume = 254 cm³

Problem 8 :

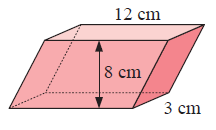
Solution :

By observing the figure, it is a parallelepiped.

Here area of cross-section is the shape of the parallelogram.

To find the volume,

Volume  =  area of cross-section × length

Volume  =  area of the parallelogram × length

=  (b × h) × length

we have,

base (b) = 12 cm, height (h) = 8 cm and length = 3 cm

Volume = (12 × 8) × 3

Volume = 288 cm³

Problem 9 :

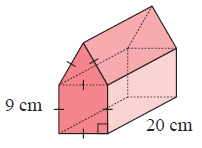
Solution :

By observing the figure, it is a house-shaped prism.

Here area of cross-section is the shape of the triangle and square.

To find the volume,

Volume  =  area of cross-section × length

Volume  =  (area of the triangle + area of the square)  × length

= (√3/4 a² + s²) × length

we have,

side (s) = 9 cm, side (a) = 9 cm and length = 20 cm

= [√3/4(9²) + 9²] × 20

= 116 × 20

Volume = 2321 cm³

Problem 10 :

A hexagon-based pyramid has a height of 54 cm. The volume of the pyramid is 1080 cm³. Calculate the area of the base of the pyramid.

Solution :

Height = 54 cm

Volume of pyramid = 1080 cm³

(1/3) x base area x height = 1080

(1/3) x base area x 54 = 1080

base area = (1080 x 3)/54

= 60 cm²

So, the required base area is 60 cm²

Problem 11 :

The Great Pyramid of Giza is a square based pyramid. The base has a side length of 440 cubits. The height of the pyramid is 280 cubits. Calculate the volume of the Great Pyramid of Giza.

Solution :

Area of square = 440 x 440

= 193600 square cubits

Volume of pyramid = (1/3) x 193600 x 280

= 18069333 cubic cubits

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.