PRACTICE QUESTIONS TO CHECK IF THE GIVEN IS FUNCTION OR NOT

Use the vertical line test to determine whether the following graph represents a function.

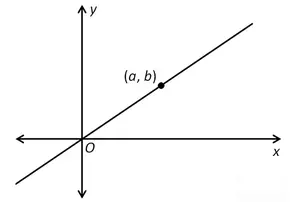
Problem 1 : 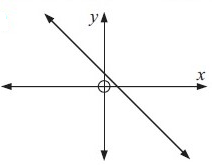Solution	Problem 2 : 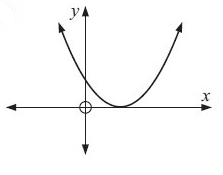Solution
Problem 3 :	Problem 4 :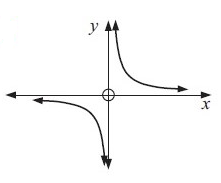
Solution	Solution
Problem 5 : 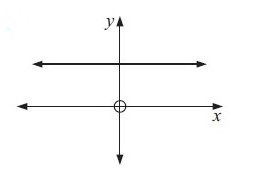Solution	Example 6 : 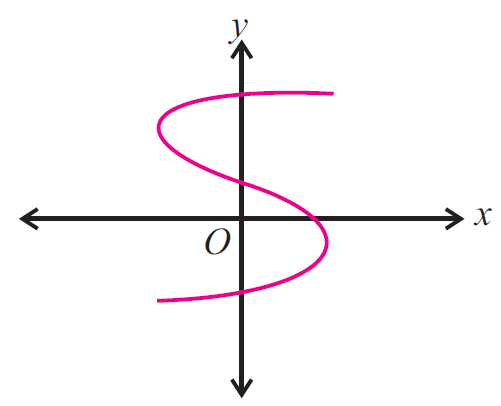Solution

Problem 7 :

Solution

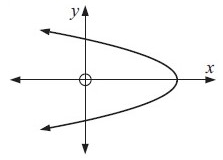
Problem 8 :

Rewrite the relation given in the scatter plot as a mapping diagram. Is this relation also a function ?

Solution

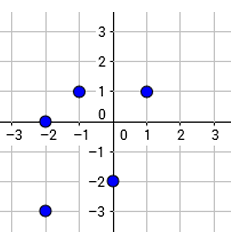
Problem 9 :

Rewrite the relation given in the scatter plot as a set of ordered pairs.

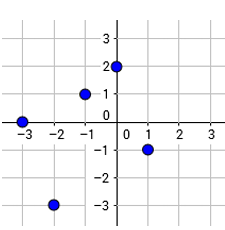
is this relation a function ?

Solution

Problem 10 :

Determine if each graph shows a function or a relation only. Then identify the domain and range.

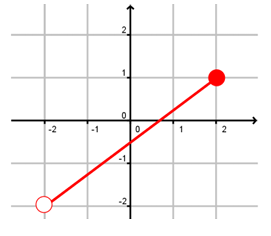
Problem 11 :

Solution

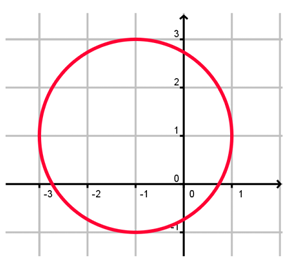
Problem 12 :

Identify the domain and range, then evaluate each function for the given value of x.

f = {(10, 7) (-2, 4) (5, 3) (4, 10)}

i)   Domain     ii)  Range     iii) f(5)

Solution

Problem 13 :

Identify the domain and range, then evaluate each function for the given value of x.

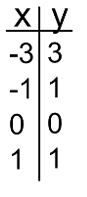
i)   Domain     ii)  Range     iii) f(1)

Solution

Problem 14 :

Identify the domain and range, then evaluate each function for the given value of x.

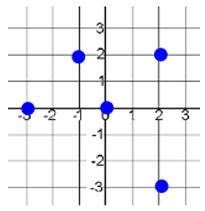
i)   Domain     ii)  Range     iii) f(-3)

Solution

Problem 15 :

Using the vertical line test, determine if the graph above shows a relation, a function, both a relation and a function, or neither a relation nor a function.

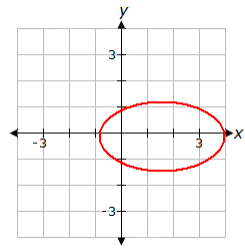
A. neither a relation nor a function

B. relation only

C. both a relation and a function

D. function only

Solution

Problem 16 :

Which of the following relations describes a function?

A. { (0, 0), (0, 2), (2, 0), (2, 2) }

B. { (2, 2), (2, 3), (3, 2), (3, 3) }

C. { (2, -1), (2, 1), (3, -1), (3, 1) }

D. { (-2, -3), (-3, -2), (2, 3), (3, 2) }

Solution

Which of the following sets of ordered pairs are functions ? Give reasons for your answers.

Problem 1 :

(1, 1), (2, 2), (3, 3), (4, 4)

Solution

Problem 2 :

(-1, 2), (-3, 2), (3, 2), (1, 2)

Solution

Problem 3 :

(2, 5), (-1, 4), (-3, 7), (2, -3)

Solution

Problem 4 :

(3, -2), (3, 0), (3, 2), (3, 4)

Solution

Problem 5 :

(-7, 0), (-5, 0), (-3, 0), (-1, 0)

Solution

Problem 6 :

(0, 5), (0, 1), (2, 1), (2, -5)

Solution

Problem 7 :

Find the range of f (x) = −x + 4 for the domain {–3, –2, –1, 1}

Solution

Problem 8 :

An employee receives a weekly salary of $340 and a 6% commission on all sales.

a. Write a rule to describe the function f(d) that gives weekly earnings in terms of d dollars in sales.

b. Find the employee’s earnings for a week with $660 total sales.

c. What were the employee’s total sales for a week in which her earnings were $1300?

Solution

Problem 9 :

Use the vertical line test to determine whether the relation is a function.

(−1, −2), (3, −1), (−5, 2) (−3, −5)

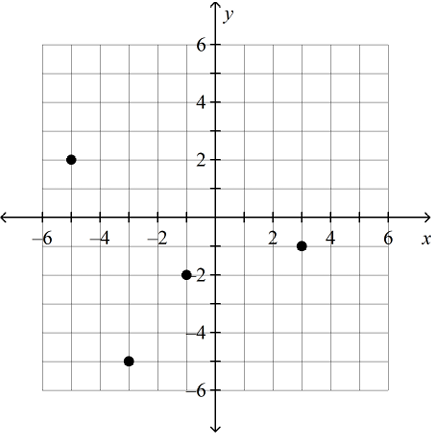
Solution

Problem 9 :

You are driving to visit a friend in another state who lives 440 miles away. You are driving 55 miles per hour and have already driven 275 miles. Write and solve an equation to find how much longer in hours you must drive to reach your destination.

Solution

Problem 10 :

A customer went to a garden shop and bought some potting soil for $17.50 and 4 shrubs. The total bill was $53.50. Write and solve an equation to find the price of each shrub.

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.