DETERMINE WHETHER THE RELATION REPRESENTS A FUNCTION

Which of the following sets of ordered pairs are functions ? Give reasons for your answers.

1)  (1, 1), (2, 2), (3, 3), (4, 4)

2)  (-1, 2), (-3, 2), (3, 2), (1, 2)

3)  (2, 5), (-1, 4), (-3, 7), (2, -3)

4)  (3, -2), (3, 0), (3, 2), (3, 4)

5)  (-7, 0), (-5, 0), (-3, 0), (-1, 0)

6)  (0, 5), (0, 1), (2, 1), (2, -5)

Problem 1 :

(1, 1), (2, 2), (3, 3), (4, 4)

Solution :

Let X be the set of inputs and Y be the set of outputs.

Inputs (x)  =  {1, 2, 3, 4}

Outputs (y)  =  {1, 2, 3, 4}

Create a mapping of the following relation,

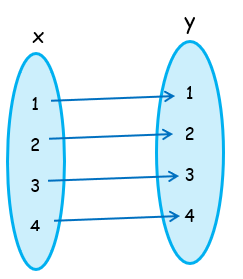
Form the arrow diagram, we understand that each x-value is being paired with only one y-value.

Or simply each input has at most one output. So, it is a function.

Problem 2 :

(-1, 2), (-3, 2), (3, 2), (1, 2)

Solution :

Let X be the set of inputs and Y be the set of outputs.

Inputs (x)  =  {-1, -3, 3, 1}

Output (y)  =  {2}

Create a mapping of the following relation,

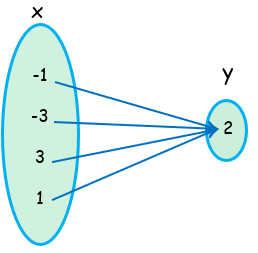
Because input has atmost only one output. So, it is a function.

Problem 3 :

(2, 5), (-1, 4), (-3, 7), (2, -3)

Solution :

Let X be the set of inputs and Y be the set of outputs.

Inputs (X)  =  {2, -1, -3, 2}

Output (Y)  =  {5, 4, 7, -3}

Create a mapping of the following relation,

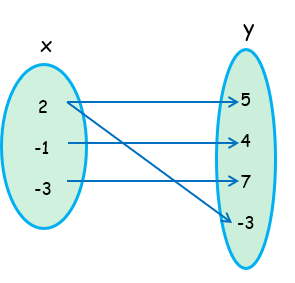
By observing the arrow diagram, one of the input has more than one output. So, it is not a function.

Problem 4 :

(3, -2), (3, 0), (3, 2), (3, 4)

Solution :

Let X be the set of inputs and Y be the set of outputs.

Inputs (x)  =  {3}

Outputs (S)  =  {-2, 0, 2, 4}

Create a mapping of the following relation,

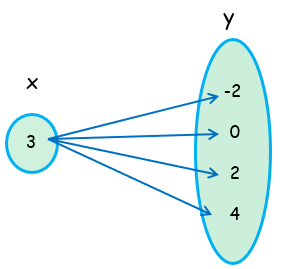
The input 3 has associate with more than one output. So, it is not a function.

Problem 5 :

(-7, 0), (-5, 0), (-3, 0), (-1, 0)

Solution :

Let X be the set of inputs and Y be the set of outputs.

The set of x  =  {-7, -5, -3, -1}

The set of y  =  {0}

Create a mapping of the following relation,

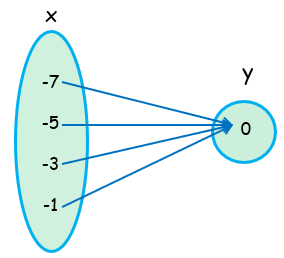
Each input is associated with only one output, but no input is having more than one output. So it is a function.

Problem 6 :

(0, 5), (0, 1), (2, 1), (2, -5)

Solution :

Let X be the set of inputs and Y be the set of outputs.

Inputs(x)  =  {0, 2}

Outputs (Y)  =  {5, 1, -5}

Create a mapping of the following relation,

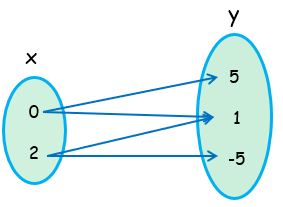
Since the inputs 0 and 2 are having more than one output, it is not a function.

Problem 7 :

Find the range of f (x) = −x + 4 for the domain {–3, –2, –1, 1}

Solution :

f(x) = -x + 4

So, the range is {7, 6, 5, 3}.

Problem 8 :

An employee receives a weekly salary of $340 and a 6% commission on all sales.

a. Write a rule to describe the function f(d) that gives weekly earnings in terms of d dollars in sales.

b. Find the employee’s earnings for a week with $660 total sales.

c. What were the employee’s total sales for a week in which her earnings were $1300?

Solution :

Let x be the total sales.

a) 

f(d) = 340 + 6% of total sales

= 340 + 6% of x

f(d) = 340 + 0.06x

So, the required function is f(d) = 340 + 0.06x.

b) Total sales = 660

f(660) = 340 + 0.06(660)

= 340 + 39.6

= 379.6

c) When total earning = 1300

f(x) = 340 + 0.06x

1300 = 340 + 0.06x

1300 - 340 = 0.06x

960 = 0.06x

x = 960/0.06

x = 16000

So, the required total sales is 16000.

Problem 9 :

Use the vertical line test to determine whether the relation is a function.

(−1, −2), (3, −1), (−5, 2) (−3, −5)

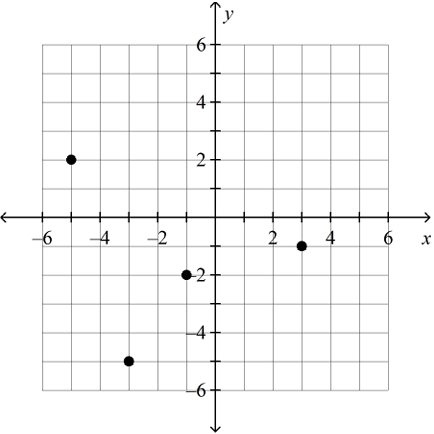
Solution :

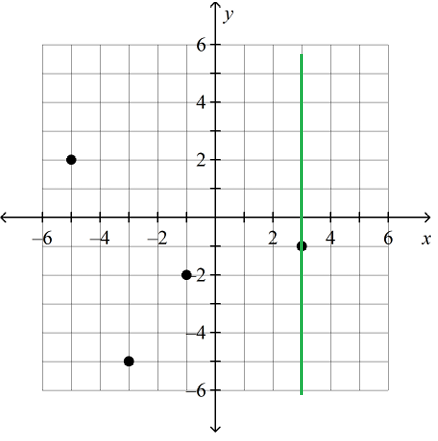
When we draw the vertical line, it is intersecting the points maximum at one point. So, this relation is function.

Problem 9 :

You are driving to visit a friend in another state who lives 440 miles away. You are driving 55 miles per hour and have already driven 275 miles. Write and solve an equation to find how much longer in hours you must drive to reach your destination.

Solution :

Total distance to be covered = 440 miles

Number of miles per hour = 55

Number of miles driven = 440 - 55x

270 = 440 - 55x

270 - 440 = -55x

-170 = -55x

x = 170/55

x = 3.09

Approximately 3 miles.

Problem 10 :

A customer went to a garden shop and bought some potting soil for $17.50 and 4 shrubs. The total bill was $53.50. Write and solve an equation to find the price of each shrub.

Solution :

Price of each shrub = x

4x + 17.50 = 53.50

4x = 53.50 - 17.50

4x = 36

x = 36/4

x = 9

So, the price of each shrub is $9.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.