DIVIDING POLYNOMIALS USING LONG DIVISION

The division of polynomials p(x) and g(x) is expressed by the following “division algorithm” of algebra.

Let p(x) and g(x) be two polynomials such that degree of p(x) ≥ degree of g(x) and g(x) ≠ 0. Then there exists unique polynomials q(x) and r (x)

such that

p(x)  =  g(x) q(x) + r (x) ... (1)

where r (x) = 0 or degree of r (x) < degree of g(x) .

The polynomial p(x) is the dividend, g(x) is the divisor, q(x) is the quotient and r (x) is the remainder.

(1) ==> Dividend = (Divisor x Quotient) + Remainder

Example 1 :

Divide the polynomial 2x³ - 6x² + 5x + 4 by (x - 2)

Solution : 

Let P(x) = 2x³ - 6x² + 5x + 4 and g(x) = x - 2

To divide the given polynomial by x - 2, we have divide the first term of the polynomial P(x) by the first term of the polynomial g(x).

If we divide 2x³ by x, we get 2x². Now we have to multiply this 2x² by x - 2. From this we get 2x³ - 4x². 

Now we have to subtract 2x³ - 4x² from the given polynomial. So we get -2x² + 5x + 4.

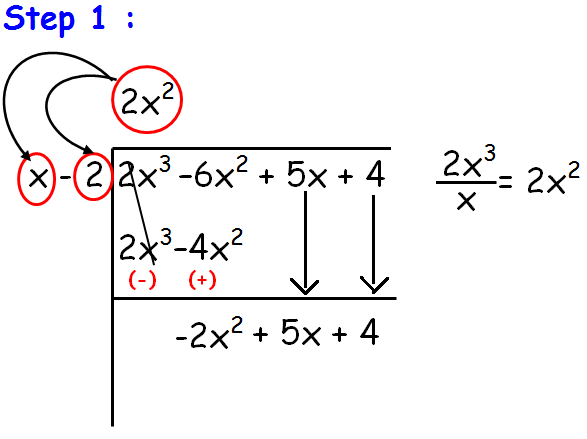
Now we have to subtract 2x³ - 4x² from the given polynomial. So we get -2x² + 5x + 4.

repeat this process until we get the degree of p(x) ≥ degree of g(x).

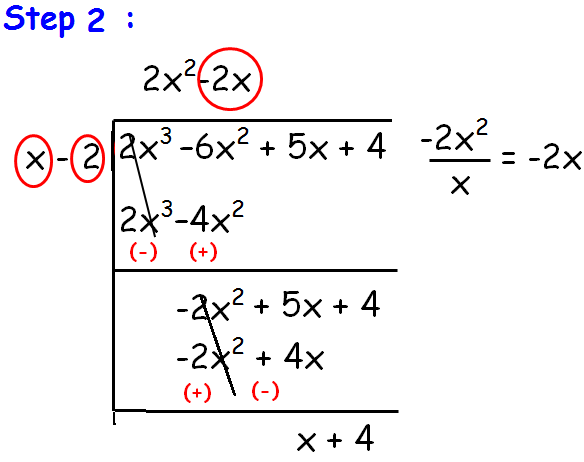
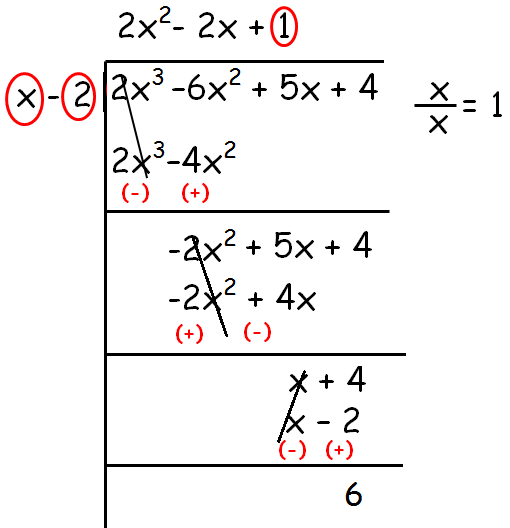
So,

Quotient  =  2x² - 2x + 1

Remainder = 6

Example 2 :

Find the quotient and remainder when 4x³ - 5x² + 6x - 2 by x - 1.

Solution :

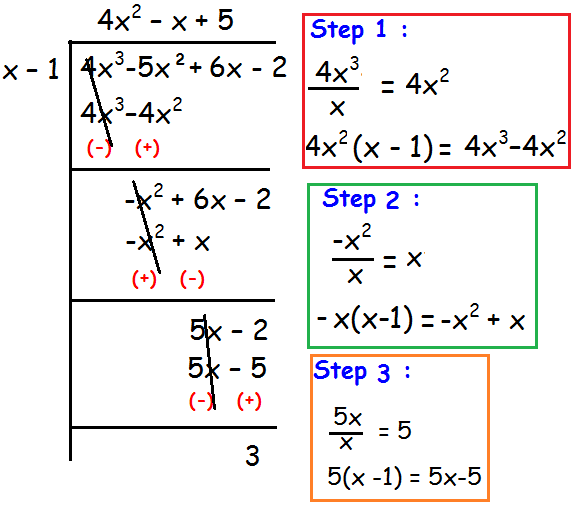
So,

Quotient  =  4x² - x + 5

Remainder  =  3

Example 3 :

Find the quotient and remainder when x³ - 7x² - x + 6 by x + 2.

Solution :

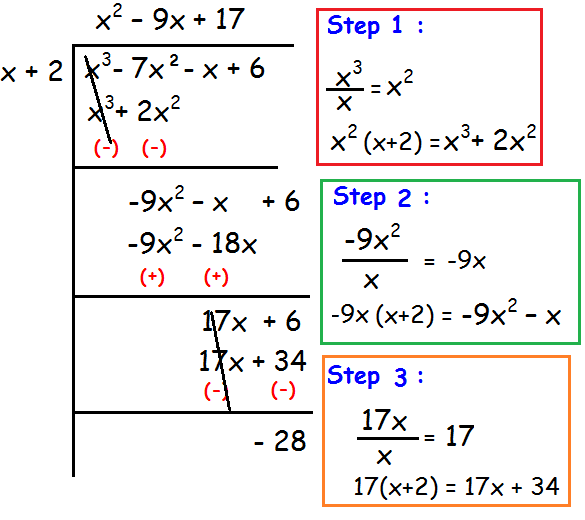
So, 

Quotient  =  x² - 9x + 17

Remainder  =  -28

Example 4 :

Find the quotient and the remainder when 10- 4x + 3x² is divided by x - 2.

Solution :

Let us first write the terms of each polynomial in descending order ( or ascending order).

Thus, the given problem becomes (10- 4x + 3x²) ÷ (x - 2)

f(x)  =  10- 4x + 3x²

=  3x² - 4x + 10

g(x) = x - 2  

Step 1 :

In the first step, we are going to divide the first term of the dividend by the first first term of the divisor.

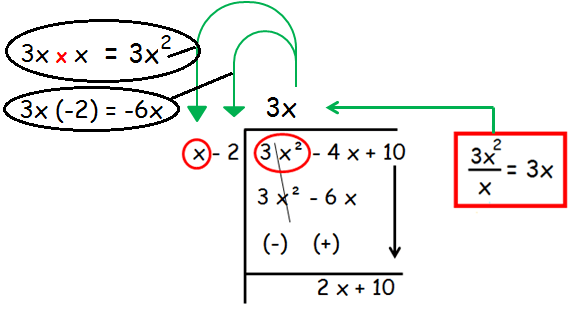
After changing the signs, +3x² and -3x² will get canceled. By simplifying, we get 2x + 10.

Step 2 :

In the second step again we are going to divide the first term that is 2x by the first term of divisor that is x.

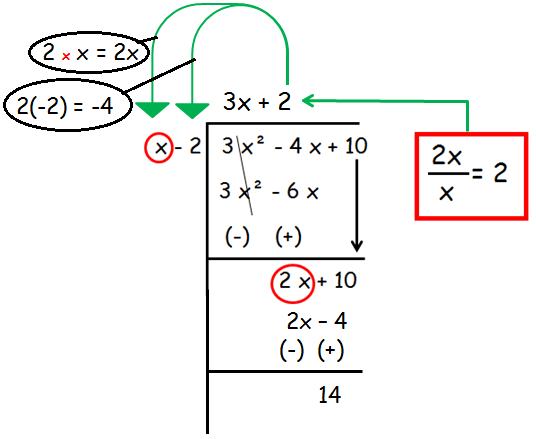
So,

Quotient  =  3x + 2

Remainder  =  14

Example 5 :

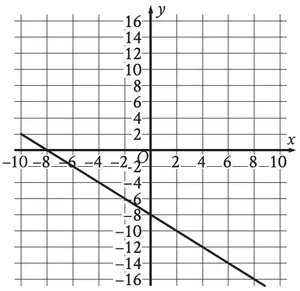
The graph represents the polynomial function

f(x) = x³ + 3x² − x − 3.

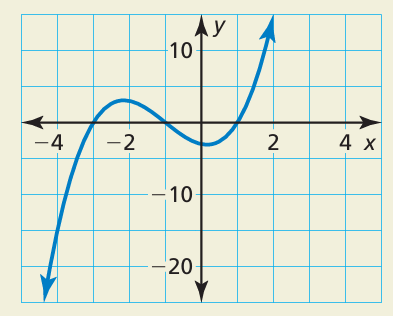
a) The expression f(x) ÷ (x − k) has a remainder of −15. What is the value of k?

b) Use the graph to compare the remainders of

(x³ + 3x² − x − 3) ÷ (x + 3)

and

(x³ + 3x² − x − 3) ÷ (x + 1)

Solution :

a) 

By observing the graph given above, we trace the point (-4, -15). When x = -4 and y = -15. So, we divide the polynomial f(x) by x + 4 to get the remainder -15.

b) 

• When divisor is x + 3, then x + 3 = 0 and x = -3. We trace the point (-3, 0). The remainder is 0 when dividing the polynomial by x + 3.
• When divisor is x + 1, then x + 1 = 0 and x = -1. We trace the point (-1, 0). The remainder is 0 when dividing the polynomial by x + 1.

Example 6 :

If x + 3 is a factor of f(x) = ax² + bx - 15 in which a and b are constants, what is the value of 3a - b ?

Solution :

f(x) = ax² + bx - 15

x + 3 is a factor the remainder will become 0.

x + 3 = 0 and x = -3

f(-3) = a(-3)² + b(-3) - 15

0 = 9a - 3b - 15

9a - 3b = 15

Dividing by 3, we get 

3a - b = 15

So, the value of 3a - b is 15.

Example 7 :

The volume V of the rectangular prism is given by

V = 2x³ + 17x² + 46x + 40

Find an expression for the missing dimension.

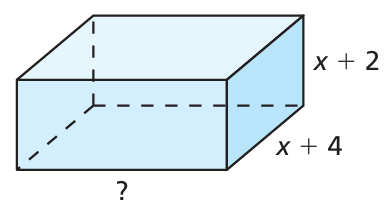
Solution :

Length = ?

Width = x + 4 and 

height = x + 2

length ⋅ width ⋅ height = volume of rectangular prism

length ⋅ width ⋅ height = 2x³ + 17x² + 46x + 40

length ⋅ (x + 4) ⋅ (x + 2) = 2x³ + 17x² + 46x + 40

length ⋅ (x² + 2x + 4x + 8) = 2x³ + 17x² + 46x + 40

length = (2x³ + 17x² + 46x + 40) / (x² + 2x + 4x + 8)

= (2x³ + 17x² + 46x + 40) / (x² + 6x + 8)

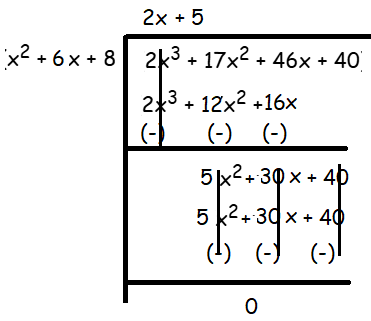
You divide two polynomials and obtain the result

5x² − 13x + 47 − [102/(x + 2)]

What is the dividend? How did you find it?

Solution :

= 5x² − 13x + 47 − [102/(x + 2)]

=  [(5x² − 13x + 47)(x + 2) - 102]/(x + 2)

= (5x³ -13x² + 47x + 10x² - 26x + 94 - 102) / (x + 2)

= (5x³ -3x² + 21x - 8) / (x + 2)

So, the dividend is 5x³ -3x² + 21x - 8.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.