ORDERING TRIANGLE SIDES AND ANGLES WORKSHEET

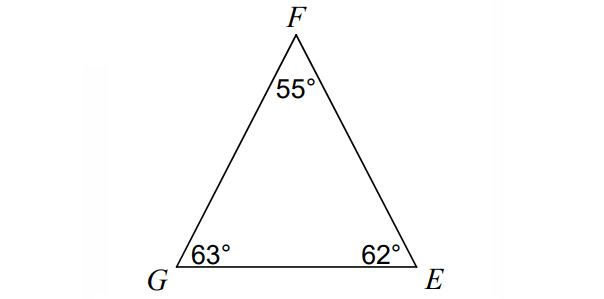
1. In ΔGEF below, order the sides from shortest to longest.

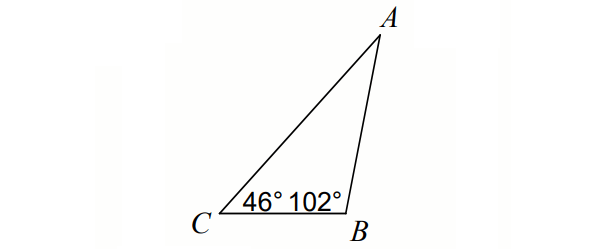
2. In ΔABC below, order the sides from longest to shortest.

3. In ΔEFD below, order the sides from shortest to longest.

4. In ΔJKL below, order the angles from smallest to greatest.

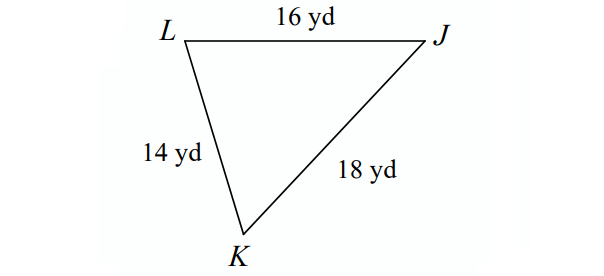
5. In ΔKLM below, KL = 18 cm, LM = 20 cm and KM = 13 cm. Order the angles from largest to smallest.

6. In ΔABC, AB is the longest side and m∠B = 70°. Find the range of possible measures for angle A. 

7. In ΔWXY, WY is the shortest side and m∠W = 30°. Find the range of possible measures for angle Y. 

8. Find the value of x and list the sides of ΔABC in order from shortest to longest if the angles have the indicated measures.

∠L = (4x + 50)°

∠M = (7x - 38)°

∠N = (2x + 12)°

1. Answer :

Order the angles from smallest to largest :

55°, 62°, 63°

The side opposite to the smallest angle is the shortest side and the side opposite to the largest angle is the longest side. 

side opposite to 55° ----> GE

side opposite to 62° ----> GF

side opposite to 63° ----> EF

Order of the sides from shortest to longest :

GE, GF, EF

2. Answer :

In ΔABC above,

m∠A + m∠B + m∠C = 180°

Substitute m∠B = 102° and m∠C = 46°.

m∠A + 102° + 46° = 180°

m∠A + 148° = 180°

Subtract 148° from each side.

m∠A = 32°

Order the angles from smallest to largest :

32°, 46°, 102°

side opposite to 102° ----> AC

side opposite to 46° ----> AB

side opposite to 32° ----> BC

Order of the sides from longest to shortest : 

AC, AB, BC

3. Answer :

m∠E = 48° and the remaining two angles m∠F and m∠D are equal, that is 66°. 

side opposite to m∠E ----> FD

side opposite to m∠F ----> ED

side opposite to m∠D ----> EF

In ΔEFD above, the shortest side is FD and the remaining two sides ED and EF are equal in length.

4. Answer :

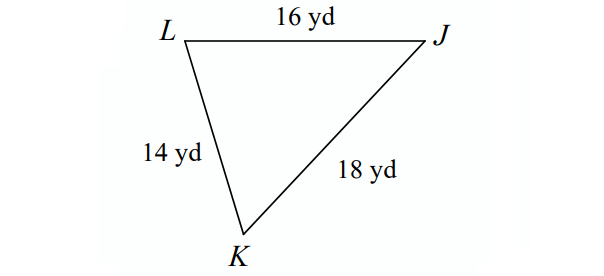
Order the sides from shortest to longest :  

14 yd, 16 yd, 18 yd

The angle opposite to the shortest side is the smallest angle and the side opposite to the longest side is the largest angle.

angle opposite to the side 14 yd long ----> ∠J

angle opposite to the side 16 yd long ----> ∠K

angle opposite to the side 18 yd long ----> ∠L

Order of the angles from smallest to largest :

∠J, ∠K, ∠L

5. Answer :

Draw ΔKLM with the given measures.

KL = 18 cm, LM = 20 cm, KM = 13

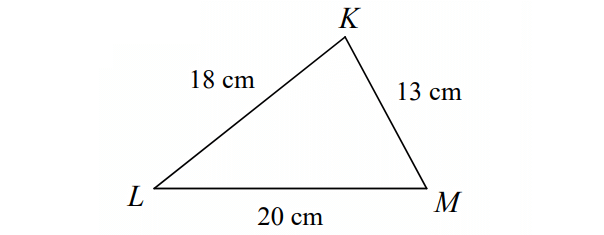
Order the sides from longest to shortest :

20 cm, 18 cm, 13 cm

angle opposite to the side 20 cm long ----> ∠K

angle opposite to the side 18 cm long ----> ∠M

angle opposite to the side 13 cm long ----> ∠L

Order of the angles from smallest to largest :

∠K, ∠M, ∠L

6. Answer :

Draw ΔABC with AB as the longest side and m∠B = 70°. 

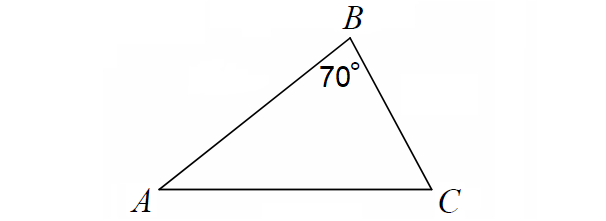
Since AB is the longest side, angle ∠C which is opposite to the side AB is the largest angle. 

m∠C > m∠B

m∠C > 70°

In ΔABC above, 

m∠A + 70° + m∠C = 180°

m∠A + m∠C = 110°

Since m∠C > 70°,

0° < m∠A < 40°

7. Answer :

Draw ΔWXY with WY as the shortest side and m∠W = 30°. 

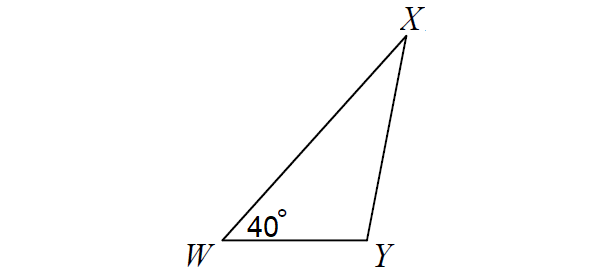
Since WY is the shortest side, angle ∠X which is opposite to the side WY is the smallest angle. 

m∠X < m∠W

m∠X < 30°

In ΔWXY above, 

40° + m∠X + m∠Y = 180°

m∠X + m∠Y = 140°

Since m∠X < 30°,  

110° < m∠Y < 140°

8. Answer :

∠L = (4x + 50)°

∠M = (7x - 38)°

∠N = (2x + 12)°

In ΔKLM, 

∠L + ∠M + ∠N = 180°

(4x + 50)° + (4x + 50)° + (2x + 12)° = 180°

4x + 50 + 7x - 38 + 2x + 12 = 180

13x + 24 = 180

13x = 156

x = 12

∠L = (4x + 50)° = 98°

∠M = (7x - 38)° = 46°

∠N = (2x + 12)° = 36°

Draw ΔLMN with the angle measures 98°, 46° and 30°. 

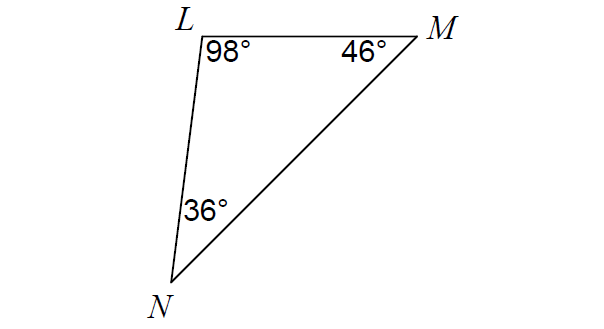
Order the angles from smallest to largest :

36°, 46°, 98°

side opposite to 36° ----> LM

side opposite to 46° ----> LN

side opposite to 98° ----> MN

Order of the sides from shortest to longest :

LM, LN, MN

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.