OPERATIONS ON RATIONAL NUMBERS WORKSHEET

Problem 1 :

Add :

⅖, ⅗

Problem 2 :

Add :

-⁵⁄₁₃, ⁷⁄₁₃, -⁹⁄₁₃

Problem 3 :

Add :

-²⁄₉, -⁵⁄₃, ⁷⁄₁₂

Problem 4 :

Subtract ⅗ from ⁷⁄₅.

Problem 5 :

Subtract ⅛ from ⅓.

Problem 6 :

Subtract ¹⁄₂₀ from ⁵⁄₁₂.

Problem 7 :

Convert the fraction ¹⁷⁄₅ to mixed number.

Problem 8 :

Convert the mnixed number 2⅗ to improper fraction.

Problem 9 :

Multiply ⅔ and ⅘.

Problem 10 :

Multiply 7 and ⁵⁄₁₄.

Problem 11 :

Divide 6 by ⅖.

Problem 12 :

Divide ⅕ by ³⁄₇.

Problem 13 :

Simplify.

Problem 14 : 

Lily earned $54 mowing lawns in two days. She worked 2.5 hours yesterday and 4.25 hours today. If Naomi was paid the same amount for every hour she works, how much did she earn per hour ?

Problem 15 : 

David traveled from A to B in 3 hours at the rate of 50 miles per hour. Then he traveled from B to C in 2 hours at the rate of 60 miles per hour. What is the average speed of David from A to C ?

Problem 16 : 

Each part of a multipart question on a test is worth the same number of points. The whole question is worth 37.5 points. Daniel got 1/2 of the parts of a question correct. How many points did Daniel receive ?

Problem 17 : 

The bill for a pizza was $14.50. Charles paid for ⅗ of the bill. How much did he pay ?

Answers

1. Answer :

2. Answer :

3. Answer :

Least common multiple of (9, 3, 12) = 36.

4. Answer :

5. Answer :

Least common multiple of (3, 8) = 24.

6. Answer :

Least common multiple of (12, 20) = 60.

7. Answer :

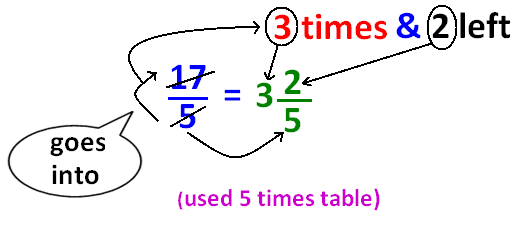
8. Answer :

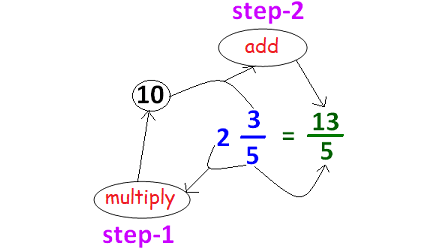
9. Answer :

10. Answer :

11. Answer :

12. Answer :

13. Answer :

14. Answer :

Analyze Information :

Identify the important information.

• Naomi made $54 mowing lawns.

• Naomi worked 2.5 hours yesterday and 4.25 hours today.

• We are asked to find how much she earned per hour

Formulate a plan :

• The total amount she earned divided by the total hours she worked gives the amount she earns per hour.

• Use the expression 54 ÷ (2.5 + 4.25) to find the amount she earned per hour.

Solve : 

Follow the order of operations.

(2.5 + 4.25) = 6.75  ----> (Add inside parentheses)

54 ÷ 6.75 = 8 ----> (Divide)

Lily earned $8 per hour mowing lawns.

15. Answer :

Analyze Information :

Identify the important information.

• David traveled from A to B in 3 hours @ 50 mph.

• David traveled from B to C in 2 hours @ 60 mph.

• We are asked to find the average speed from A to C.

Formulate a plan :

• The total distance covered from A to C divided by total time taken gives the average speed from A to C.

• Use the expression (3 x 50) + (2 x 60)  to find the total distance from A to C.

That is, 270 miles

• Use the expression (3 + 2)  to find the total time taken from A to C. 

That is, 5 hours

Solve : 

Divide the total distance (A to C) by the total time taken (A to C)

270 ÷ 5 = 54 ----> (Divide)

So, the average speed from A to C is 54 miles per hour.

16. Answer :

To find the total points received by Daniel, we have to multiply ½ and 37.5  

Step 1 :

Convert the decimal 3.75 as the fraction 75/2

½ x 37.5 = ½ x ⁷⁵⁄₂

Step 2 :

Multiply. Write the product in simplest form.

½ x ⁷⁵⁄₂ = ⁷⁵⁄₄ = 18¾

So, Daniel received 18¾ points. 

17. Answer :

To find the amount paid by Charles, we have to multiply 3/5 and 14.50  

Step 1 :

Convert the decimal 14.50 as the fraction 29/2

⅗ x 14.50 = ⅗ x ²⁹⁄₂

Step 2 :

Multiply. Write the product in simplest form.

⅗ x ²⁹⁄₂ = ⁸⁷⁄₁₀ = 8⁷⁄₁₀

Hence, Charles paid $8⁷⁄₁₀. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.