OPERATIONS ON POLYNOMIALS WORKSHEET

1. Add : (5x² + 4x + 1) + (2x² + 5x + 2)

2. Subtract (2x² + 2y² - 6) from  (3x² - 7y² + 9).

3. Multiply : (3x³)(6x⁴)

4. Multiply using distributive property : (x + 3)(x - 6)

5. Multiply using FOIL method : (x + 4)(x + 5)

6. Multiply : 5(3x² + 5x + 7)

7. Multiply : (x + 3)(x² - 5x + 7)

8. Divide (x³ - 4x² + 6x) by x, where x ≠ 0.

9. Divide (x² - 9) by (x - 3), where x ≠ 3.

10. Find the quotient and the remainder when the polynomial (5x² - 7x + 2) is divided by (x - 1), using long division. 

11.  (x² y - 3y² + 5xy²) - (-x²y + 3xy² - 3y²)

which of the following is equivalent to the expression above.

a)  4x2y2      b)  8xy² - 6y²         c)  2x²y + 2xy²

d)  2x² y - 6y² 

12.  For a polynomial p(x), the value of p(3) is -2. Which of the following must be true about p(x) ?

a) x - 5 is a factor of p(x)

b)  x - 2 is a factor of p(x)

c) x + 2 is a factor of p(x)

d) The remainder when p(x) is divided by x - 3 is -2.

13.  9a⁴ + 12a² b² + 4b⁴

which of the following is equivalent to the expression shown above ?

a) (3a² + 2b²)²          b) (3a + 2b)⁴     c)  (9a² + 4b²)²

d)  (9a + 4b)⁴

14.  2x(2x + 5) + 3(3x + 5) = ax² + bx + c

In the equation above, a, b and c are constants, if the equation is true for all values of x, what is the value of b ?

1. Answer :

Associative and Commutative Properties can be used to regroup the like terms together and combine them as shown below.  

= (5x² + 4x + 1) + (2x² + 5x + 2)

= (5x² + 2x²) + (4x + 5x) + (1 + 2)

= 7x² + 9x + 3

2. Answer : 

= (3x² - 7y² + 9) - (2x² + 2y² - 6)

Distributive Property. 

= 3x² - 7y² + 9 - 2x² - 2y² + 6

Group like terms together. 

= (3x² - 2x²) + (-7y² - 2y²) + (9 + 6)

Combine like terms. 

= x² - 9y² + 15

3. Answer :

= (3x³)(6x⁴)

Group factors with like bases together. 

= (3 ⋅ 6)(x³ ⋅ x⁴)

Use the Product of Powers Property. 

= 18x^{3 + 4}

= 18x⁷

4. Answer : 

= (x + 3)(x - 6)

Distribute. 

= x(x - 6) + 3(x - 6)

Distribute again. 

= x(x) + x(-6) + 3(x) + 3(-6)

Multiply. 

= x² - 6x + 3x - 18

Combine like terms. 

= x² - 3x - 18

5. Answer : 

Multiply the First terms :

(x + 4)(x + 5) ---> x ⋅ x = x²

Multiply the Outer terms :

(x + 4)(x + 5) ---> x ⋅ 5 = 5x

Multiply the Inner terms :

(x + 4)(x + 5) ---> 4 ⋅ x = 4x

Multiply the Last terms :

(x + 4)(x + 5) ---> 4 ⋅ 5 = 20

(x + 4)(x + 5) = x² + 5x + 4x + 20

(x + 4)(x + 5) = x² + 9x + 20

6. Answer : 

= 5(3x² + 5x + 7)

Distribute 2.

= 5(3x²) + 5(5x) + 5(7)

Multiply. 

= 15x² + 25x + 35

7. Answer :

= (x + 3)(x² - 5x + 7)

Distributive. 

= x(x² - 5x + 7) + 3(x² - 5x + 7)

Distribute again. 

= x(x²) + x(-5x) + x(7) + 3(x²) + 3(-5x) + 3(7)

Simplify. 

= x³ - 5x² + 7x + 3x² - 15x + 21

Combine the like terms.

= x³ - 5x²  + 3x²+ 7x - 15x + 21

= x³ - 2x² - 8x + 21

8. Answer : 

= (x³ - 4x² + 6x)/x

= x³/x - 4x²/x + 6x/x

= x² - 4x + 6

9. Answer : 

= (x² - 9)/(x - 3)

= (x² - 3²)/(x - 3)

Using the algebraic identity a² - b² = (a + b)(a - b) to factor (x² - 3²). 

= [(x + 3)(x - 3)]/(x - 3)

= x + 3

10. Answer : 

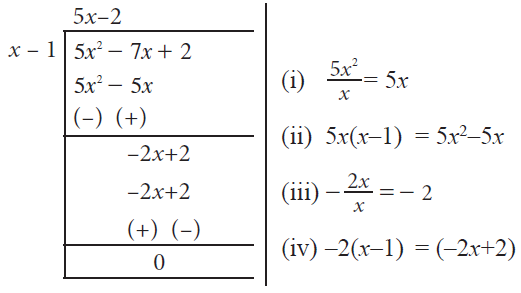
Quotient = 5x - 2

Remainder = 0

11. Answer : 

= (x² y - 3y² + 5xy²) - (-x²y + 3xy² - 3y²)

Distributing negative, we get

= x² y - 3y² + 5xy² + x²y - 3xy² + 3y²

Combining the like terms, we get

= x² y + x²y - 3y² + 3y² + 5xy²  - 3xy² 

= 2x² y + 2xy²

So, option c is correct.

12. Answer : 

For a polynomial p(x),

when p(1) = 0 then x = 1 is a solution or zero.

When p(1) = a, then x = 1 is not a solution and dividing the polynomial by x - 1 we get the remainder a.

So, option d is correct.

13. Answer : 

= 9a⁴ + 12a² b² + 4b⁴

= 3²(a²) ² + 12a² b² + 2²(b²)²

= (3a²) ² + 12a² b² + (2b²)²

= (3a²) ² + 2(3a²) (2b²) + (2b²)²

Looks like an algebraic identity a² + 2ab + b²

= (3a² + 2b²)²

14. Answer : 

2x(2x + 5) + 3(3x + 5) = ax² + bx + c

Using distributive property,

4x² + 10x + 9x + 15 = ax² + bx + c

Combining the like terms, we get

4x² + 19x + 15 = ax² + bx + c

Comparing the corresponding terms

a = 4, b = 19 and c = 15

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.