NUMBER OF SOLUTIONS OF LINEAR SYSTEM

The graph of the system is a pair of lines that intersect in one point.

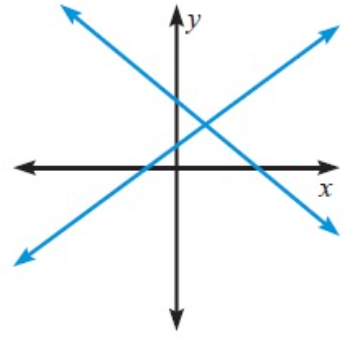
The graph of the system is a pair of lines that intersect in one point.

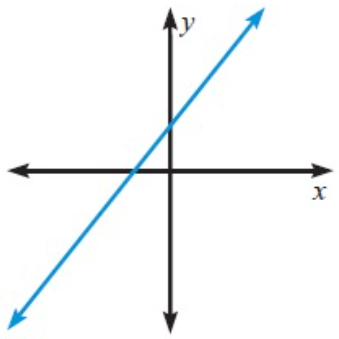
The graph of the system is a pair of parallel lines so that there is no point of intersection.

Without solving the equations completely, we can find how many solutions they will have.

The general form of a pair of linear equations is

a₁x + b₁y + c₁  =  0

a₂x + b₂y + c₂  =  0

(where a₁, a₂, b₁, b₂, c₁, and c₂ are real numbers)

If a pair of linear equations is given by 

a₁x + b₁y + c₁  =  0

a₂x + b₂y + c₂  =  0

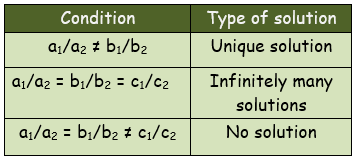
We have to check the condition then follow solutions.

Example 1 :

2x – y  =  -5

x + 2y  =  0

Solution :

By writing the given equations a₁x + b₁y + c₁  =  0 and a₂x + b₂y + c₂  =  0 in the form, we get

2x – y + 5  =  0

x + 2y + 0  =  0

From the equations, let us find the values of a₁, a₂, b₁, b₂, c₁, and c₂

Here a₁  =  2, b₁  =  -1 and c₁  =  5

a₂  =  1, b₂  =  2 and c₂  =  0

a₁/a₂  =  2/1 -----(1)

b₁/b₂  =  -1/2 -----(2)

c₁/c₂  =  5/0 -----(3)

 (1) ≠ (2)

Now, a₁/a₂ ≠ b₁/b₂

So, it has unique solution.

Example 2 :

-2x + 3y  =  12

2x - 3y  =  6

Solution :

-2x + 3y – 12  =  0

2x - 3y – 6  =  0

From the equations, let us find the values of a₁, a₂, b₁, b₂, c₁, and c₂

Here a₁  =  -2, b₁  =  3 and c₁  =  -12

a₂  =  2, b₂  =  -3 and c₂  =  -6

a₁/a₂  =  -2/2  =  -1 -----(1)

b₁/b₂  =  -3/3  =  -1 -----(2)

c₁/c₂  =  12/6  =  2 -----(3)

 (1) = (2) ≠ (3)

Now, a₁/a₂  =  b₁/b₂ ≠ c₁/c₂

So, it has no solution.

Example 3 :

2x - y  =  5

-4x + 2y  =  -10

Solution :

2x - y – 5  =  0

-4x + 2y + 10  =  0

Here a₁  =  2, b₁  =  -1 and c₁  =  -5

a₂  =  -4, b₂  =  2 and c₂  =  10

a₁/a₂  =  -2/4  =  -1/2 -----(1)

b₁/b₂  =  -1/2 -----(2)

c₁/c₂  =  -5/10  =  -1/2 -----(3)

 (1)  =  (2)  =  (3)

Now, a₁/a₂  =  b₁/b₂  =  c₁/c₂

So, the given equations are infinitely many solutions.

Example 4 :

x + 5y  =  -12

x - 5y  =  8

Solution :

By writing the given equations a₁x + b₁y + c₁  =  0 and a₂x + b₂y + c₂  =  0 in the form, we get

x + 5y + 12  =  0

x - 5y - 8  =  0

Here a₁  =  1, b₁  =  5 and c₁  =  12

a₂  =  1, b₂  =  -5 and c₂  =  -8

a₁/a₂  =  1/1  =  1 -----(1)

b₁/b₂  =  -5/5  =  -1 -----(2)

c₁/c₂  =  -12/8  =  -3/4 -----(3)

 (1) ≠ (2)

Now, a₁/a₂ ≠ b₁/b₂ 

So, it has unique solution.

Example 5 :

-x + 5y  =  8

2x - 10y  =  7

Solution :

-x + 5y - 8  =  0

2x - 10y - 7  =  0

Here a₁  =  -1, b₁  =  5 and c₁  =  -8

a₂  =  2, b₂  =  -10 and c₂  =  -7

a₁/a₂  =  -1/2 -----(1)

b₁/b₂  =  -5/10  =  -1/2 -----(2)

c₁/c₂  =  8/7 -----(3)

 (1) = (2) ≠ (3)

Now, a₁/a₂  =  b₁/b₂ ≠ c₁/c₂

So, it has no solution.

Example 6 :

4x - 7y  =  27

-6x - 9y  =  -21

Solution :

4x - 7y - 27  =  0

-6x - 9y + 21  =  0

Here a₁  =  4, b₁  =  -7 and c₁  =  -27

a₂  =  -6, b₂  =  -9 and c₂  =  21

a₁/a₂  =  -4/6  =  -2/3 -----(1)

b₁/b₂  =  -7/9 -----(2)

c₁/c₂  =  -27/21  =  -9/7 -----(3)

 (1) ≠ (2)

Now, a₁/a₂ ≠ b₁/b₂ 

So, it has unique solution.

Example 7 :

For the linear system 2x + 3y = 12 and 4x + 6y = C, what value(s) of C will give the system

a) an infinite number of solutions?

b) no solution?

Solution :

2x + 3y = 12 and 4x + 6y = C

a₁/a₂ = 2/4

b₁/b₂ = 3/6

c₁/c₂ = 12/C

a) Infinite number of solution :

a₁/a₂ = b₁/b₂ = c₁/c₂

2/4 = 3/6 = 12/C

1/2 = 12/C

C = 12(2)

C = 24

So, the value of C is 24.

b) No solution :

a₁/a₂ = b₁/b₂ ≠ c₁/c₂

3/6 ≠ 12/C

1/2 ≠ 12/C

C ≠ 24

So, the value of C is other than 24.

Example 8 :

Suppose you are given only the following pieces of information about a system of linear equations. Would you be able to predict the number of solutions to the system? Explain.

a) The slopes of the lines are the same.

b) The y-intercepts of the lines are the same.

c) The x-intercepts are the same, and the y-intercepts are the same.

Solution :

a) The slopes of the lines are the same.

If the slopes are equal, then it must be parallel line. Then there must be no solution.

b) The y-intercepts of the lines are the same.

Since the y-intercepts are the same, they may have same slopes or different slopes.

• If slopes and y-intercepts are equal, then it may have infinite number of solutions.
• If slopes are not same then it may have unique solution. The solution is at y-intercept.

c) The x-intercepts are the same, and the y-intercepts are the same.

Since x-intercepts and y-intercepts are the same, then it must be the same line. So, it will have infinite number of solution.

Note :

To find the point of intersections particularly, we can use the following methods.

• Substitution Method
• Elimination Method
• Cross multiplication method

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.