NATURE OF THE ROOTS OF A QUADRATIC EQUATION

In this section, we will examine the roots of a quadratic equation.

That is, we will analyze whether the roots of a quadratic equation are equal or unequal,  real or imaginary and rational or irrational. 

To examine the roots of a quadratic equation, let us consider the general form a quadratic equation.

 ax² + bx + c = 0

(Here a, b and c are real and rational numbers)

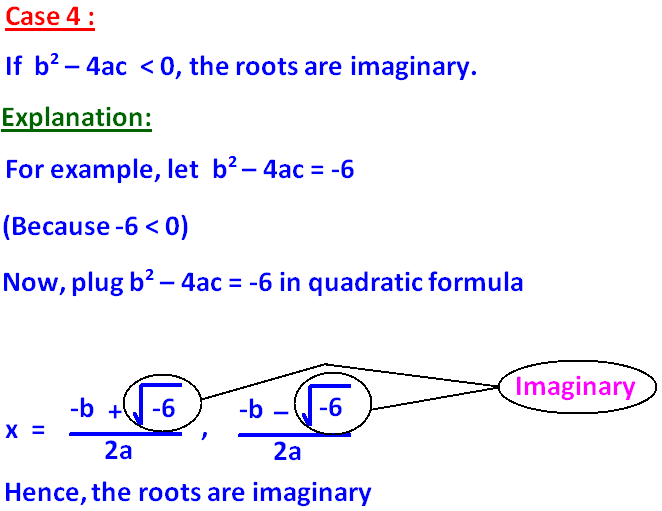
To know the nature of the roots of a quadratic-equation, we will be using the discriminant b² - 4ac.

Because b² - 4ac discriminates the nature of the roots.

Let us see how this discriminant b² - 4ac can be used to know the nature of the roots of a quadratic-equation.

Examples 1-5 : Examine the nature of the roots of the quadratic equation.

Example 1 :

3x² + 8x + 4 = 0

Solution :

The given quadratic equation is in general form

ax² + bx + c = 0

Then, we have a = 3, b = 8 and c = 4.

Find the value of the discriminant b² - 4ac. 

b² - 4ac = 8² - 4(3)(4)

b² - 4ac = 64 - 48

b² - 4ac = 16 

Here, b² - 4ac > 0 and also a perfect square. 

So, the roots are real, unequal and rational.  

Example 2 :

2x² - 3x - 1 = 0 

Solution :

The given quadratic equation is in general form

ax² + bx + c = 0

Then, we have a = 2, b = -3 and c = -1.

Find the value of the discriminant b² - 4ac. 

b² - 4ac = (-3)² - 4(2)(-1)

b² - 4ac = 9 + 8

b² - 4ac = 17 

Here, b² - 4ac > 0, but not a perfect square. 

So, the roots are real, unequal and irrational.  

Example 3 :

x² - 16x + 64 = 0

Solution :

The given quadratic equation is in general form

ax² + bx + c = 0

Then, we have a = 1, b = -16 and c = 64.

Find the value of the discriminant b² - 4ac. 

b² - 4ac = (-16)² - 4(1)(64)

b² - 4ac = 256 - 256

b² - 4ac = 0 

So, the roots are real, equal and rational.  

Example 4 :

5x² - 4x + 2 = 0

Solution :

The given quadratic equation is in general form

ax² + bx + c = 0

Then, we have a  =  5, b  =  -4 and c  =  2.

Find the value of the discriminant b² - 4ac. 

b² - 4ac = (-4)² - 4(5)(2)

b² - 4ac = 16 - 40

b² - 4ac = -24 

Here, b² - 4ac < 0. 

So, the roots are imaginary. 

Example 5 : 

1/(x + 1) + 2/(x - 4) = 2

Solution :

The given quadratic equation is not in general form.

First, write the given quadratic equation in general form. 

1/(x + 1) + 2/(x - 4) = 2

Add the two fractions on the right side of the equation using cross multiplication. 

[(x - 4) + 2(x + 1)]/[(x + 1)(x - 4)] = 2

(x - 4 + 2x + 2)/(x² - 3x - 4) = 2

(3x - 2)/(x² - 3x - 4) = 2

Multiply each side by (x² - 3x - 4). 

3x - 2 = 2(x² - 3x - 4)

3x - 2 = 2x² - 6x - 8

2x² - 9x - 6 = 0

Now, the quadratic equation is general form

ax² + bx + c = 0

Then, we have a = 2, b = -9 and c = -6.

Find the value of the discriminant b² - 4ac. 

b² - 4ac = (-9)² - 4(2)(-6)

b² - 4ac = 81 + 48

b² - 4ac = 129

Here, b² - 4ac > 0, but not a perfect square. 

So, the roots are real, unequal and irrational.

Example 6 : 

x = 1 - 2y

4y = x² + 3

How many ordered pairs (x, y) in the xy-plane are solutions to the system of equations above?

A) 0

B) 1

C) 2

D) Infinitely Many

Solution :

x = 1 - 2y ----(1)

4y = x² + 3 ----(2)

(1) :

x = 1 - 2y

Add 2y to both sides.

x + 2y = 1

Subtract x from both sides.

2y = 1 - x

Multiply both sides by 2.

4y = 2 - 2x

Substitute 4y = 2 - 2x in (2).

2 - 2x = x² + 3

x² + 2x + 1 = 0

Comparing ax² + bx + c = 0 and x² + 2x + 1 = 0,

a = 1, b = 2 and c = 1

Find the value of the discriminant b² - 4ac.

b² - 4ac = 2² - 4(1)(1)

b² - 4ac = 4 - 4

b² - 4ac = 0

Here, b² - 4ac = 0. 

So, the roots are real and equal. It means, there is only one real value for x. Hence, we will have only one real value for y.

Therefore, only one ordered pair (x, y) in the xy-plane is solution to the given system of equations.

The correct answer choice is (B).

Example 7 :

2x² + 8x - m³ = 0

If the roots of the quadratic equation above are equal, then find the value of m.

Solution :

Comparing ax² + bx + c = 0 and 2x² + 8x - m³ = 0,

a = 2, b = 8 and c = -m³

Because the roots of the given equation are equal, 

b² - 4ac = 0

8² - 4(2)(-m³) = 0

64 + 8m³ = 0

Subtract 64 from both sides. 

8m³ = -64

Divide both sides by 8.

m³ = -8

m³ = (-2)³

m = -2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and Venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6