METHODS OF SOLVING QUADRATIC EQUATIONS

Example 1 :

Solve the quadratic equation by factoring :

x² – 5x – 24  =  0

Solution :

In the given quadratic equation, the coefficient of x² is 1.

Decompose the constant term -24 into two factors such that the product of the two factors is equal to -24 and the addition of two factors is equal to the coefficient of x, that is 5. 

Then, the two factors of -24 are 

+3 and -8

Factor the given quadratic equation using +3 and -8 and solve for x.

(x + 3)(x - 8)  =  0

x + 3  =  0  or  x - 8  =  0

x  =  -3  or  x  =  8

So, the solution is {-3, 8}. 

Example 2 :

Solve the quadratic equation by factoring :

3x² – 5x – 12  =  0

Solution :

In the given quadratic equation, the coefficient of x² is not 1.

So, multiply the coefficient of x² and the constant term "-12". 

3 ⋅ (-12)  =  -36

Decompose -36 into two factors such that the product of two factors is equal to -36 and the addition of two factors is equal to the coefficient of x, that is -5.

Then, the two factors of -36 are 

+4 and -9

Now we have to divide the two factors 4 and -3 by the coefficient of x², that is 3.

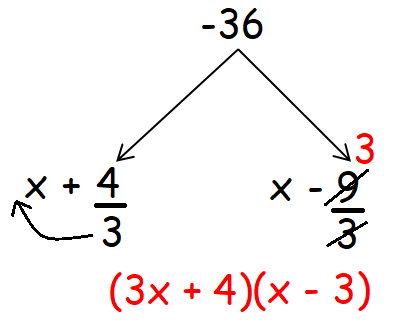
Now, factor the given quadratic equation and solve for x as shown below. 

(3x + 4)(x - 3)  =  0

3x + 4  =  0  or  x - 3  =  0

x  =  -4/3  or  x  =  3

So, the solution is {-4/3, 3}. 

Example 3 :

Solve the quadratic equation using quadratic formula :

x² – 5x – 24  =  0

Solution : 

The given quadratic equation is in the form of 

ax² + bx + c  =  0

Comparing 

x² – 5x – 24  =  0

and 

ax² + bx + c  =  0

we get 

a  =  1, b  =  -5 and c  =  -24

Substitute the above values of a, b and c into the quadratic formula. 

Therefore, the solution is

{-3, 8} 

Example 4 :

Solve the following quadratic equation by completing the square method.

9x² - 12x + 4  =  0

Solution :

Step 1 :

In the given quadratic equation 9x² - 12x + 4 = 0, divide the complete equation by 9 (coefficient of x²). 

  x² - (12/9)x + (4/9)  =  0

x² - (4/3)x + (4/9)  =  0

Step 2 :

Subtract 4/9 from each side. 

x² - (4/3)x  =  - 4/9

Step 3 :

In the result of step 2, write the "x" term as a multiple of 2. 

Then, 

x² - (4/3)x  =  - 4/9

x² - 2(x)(2/3)  =  - 4/9

Step 4 :

Now add (2/3)² to each side to complete the square on the left side of the equation.  

Then, 

x² - 2(x)(2/3) + (2/3)²  =  - 4/9 + (2/3)²

(x - 2/3)²  =  - 4/9 + 4/9

(x - 2/3)²  =  0

Take square root on both sides. 

√(x - 2/3)²  =  √0

x - 2/3  =  0

Add 2/3 to each side. 

x  =  2/3

So, the solution is 2/3. 

Example 5 :

If x² + 5x + 1 = 0, then find the value of x + 1/x.

Solution :

Given that, x² + 5x + 1 = 0

We find the value of x + 1/x,

Let us solve for x using formula,

= [-b ± √(b² - 4ac)]/2a

From the given equation, a = 1, b = 5 and c = 1

= [-5 ± √(5² - 4(1)(1))]/2(1)

= [-5 ± √(25 - 4)]/2

= [-5 ± √21]/2

When x = [-5 + √21]/2, then 1/x = 2/[-5 + √21]

x + 1/x = [-5 + √21]/2 + 2/[-5 + √21]

Example 6 :

Solve for x :

√3 x² - 2√2 x - 2√3 = 0

Solution :

√3 x² - 2√2 x - 2√3 = 0

Product of coefficient of x² and constant = -6

Middle term = - 2√2

√3 x² - 3√2x + √2 x - 2√3 = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.