MATH TERMS THAT START WITH I
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Icosahedron :
A polygon with 20 faces.

Identity :
An equality that holds regardless of the values of its variables.
Improper Fraction :
- A fraction in which the numerator is greater or equal to its denominator.
- Imperial System :
- The imperial system (plural imperial systems) A system of measurement in use in the United Kingdom and other Commonwealth countries, now mostly superseded by the metric system.
- Incenter :
- The center of the circle that is inscribed in a triangle.
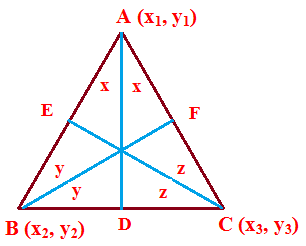
Isosceles Triangle :
A triangle with two equal sides is called isosceles triangle. The angles which are opposite to equal sides are equal. In the following triangle the sides AB and AC are equal and angles B and C are also equal.
Integers :
Integers are set of all whole numbers and their opposites. We are using number line to denote integers
....-3, -2, -1, 0, 1, 2, 3....
In the following diagram the <1 and <3 and <2 and <4 represents interior angles.

Inverse Variation :
we can say two quantities are said to be in inverse variation if one quantity increases, then the other quantity decreases or when one quantity decreases, the other quantity increases.
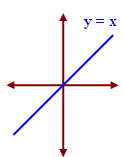
Identity Function :
A function f from a set A to the same set A is said to be identity function if f(x) = x for all x ∈ A.
If A -> A is defined by f(x) = x for all x ∈ A.
Example of identity function is y = x.
Inverse Function :
To define the inverse of a function f the function must be one-to-one and onto.
Implicit Function :
When the relation between x and y is given by an equation in the form of f(x, y) = 0 and the equation is not easily solvable for y, then y is said to be implicit function.
Infinite Set :
A set which contains uncountable elements is called as an infinite set. In other words, a set whose cardinal number is uncountable is called as an infinite set.
For example,
A = set of all whole numbers.
The cardinal number of A is not countable, so A is infinite.
Integration :
A function g(x) is called am anti derivative or integral of a function g(x) on an interval I. If g'(x) = g(x) for every value of x in I.
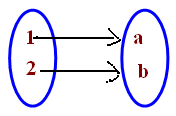
Image :
The element of B associated with x is called image of x under f.
Interval :
A subset of the real line is called interval if it contains at least two numbers it contains all numbers between the two elements.
Example of intervals
The set of all real numbers between -2 < x < 2.
Inequality :
Mathematical equation that contains greater than or less than (< or >) and not equal (≠) symbols. a < b, x+y > 2z.
Independent Variable :
A variable is said to be an independent variable if it has any arbitrary values.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
