LINEAR INEQUALITIES WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problems 1-2 : Say whether the ordered pair is a solution of the inequality.
Problem 1 :
(7, 3) ; y < x - 1
Problem 2 :
(4, 5) ; y > 3x + 2
Problems 3-4 : Graph the solutions of each linear inequality.
Problem 3 :
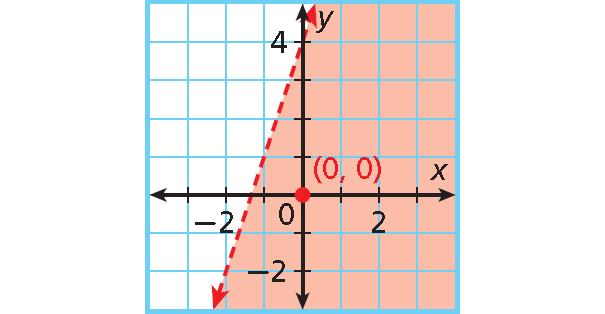
y < 3x + 4
Problem 4 :
3x + 2y ≥ 6
Problems 5-7 : Write an inequality to represent each graph.
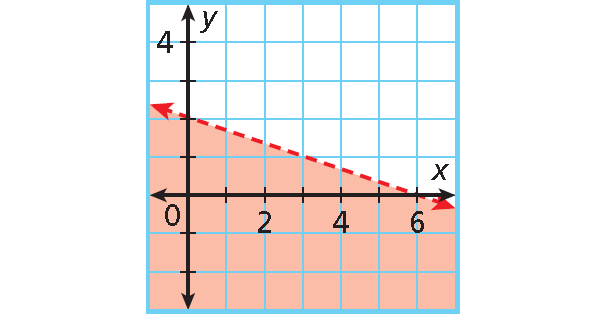
Problem 5 :
Problem 6 :
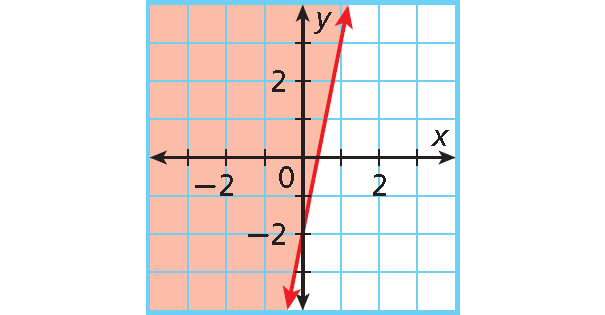
Problem 7 :
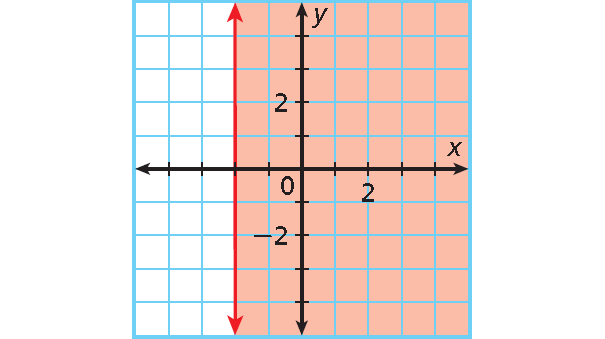
Problems 8-11 : Solve for x.
Problem 8 :
5x - 2 ≥ 4 + 3x
Problem 9 :
3x - 2 < 4 + 4x
Problem 10 :
5 - x > -7
Problem 11 :
2 - 3x ≤ 14
Problem 12 :
(2x - 3)/4 + 9 ≥ 3 + 4x/3
Problem 13 :
Lily can spend at most $7.50 on vegetables for a party. Broccoli costs $1.25 per bunch and carrots cost $0.75 per package.
A. Write a linear inequality to describe the situation.
B. Graph the solutions.
C. Give two combinations of vegetables that Sarah can buy.

1. Answer :
Substitute 7 for x and 3 for y in the given inequality.
3 < 7 - 1
3 < 4 ✓
(7, 3) is a solution.
2. Answer :
Substitute 4 for x and 5 for y in the given inequality.
5 > 3(4) + 2
5 > 12 + 2
5 > 14 ✗
(4, 5) is not a solution.
3. Answer :
Step 1 :
The inequality is already solved for y.
Step 2 :
Graph the boundary line y = 3x + 4. Use a dashed line for <.
Step 3 :
The inequality is <, so shade below the line.
4. Answer :
Step 1 :
Solve the inequality for y.
3x + 2y ≥ 6
2y ≥ 6 - 3x
y ≥ 3 - (3/2)x
y ≥ -(3/2)x + 3
Step 2 :
Graph the boundary line y = -(3/2)x + 3. Use a solid line for ≥.
Step 3 :
The inequality is ≥, so shade above the line.
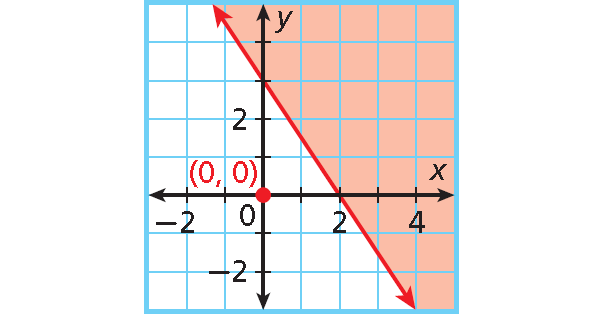
5. Answer :
y-intercept : 2; slope : - 1/3.
Write an equation in slope-intercept form.
y = mx + b ---> y = -(1/3)x + 2
The graph is shaded below a dashed boundary line.
Replace = with < to write the inequality y < -(1/3)x + 2.
6. Answer :
y-intercept : -2; slope : 5.
Write an equation in slope-intercept form.
y = mx + b ---> y = 5x + (-2)
The graph is shaded above a solid boundary line.
Replace = with ≥ to write the inequality y ≥ 5x - 2.
7. Answer :
y-intercept : none; slope : undefined.
The graph is a vertical line at x = -2.
The graph is shaded on the right side of a solid boundary line.
Replace = with ≥ to write the inequality x ≥ - 2.
8. Answer :
5x - 2 ≥ 4 + 3x
Subtract 3x from both sides.
2x - 2 ≥ 4
Add 2 to both sides.
2x ≥ 6
Divide both sides by 2.
x ≥ 3
9. Answer :
3x - 2 < 4 + 4x
Subtract 4x from both sides.
-x - 2 < 4
Add 2 to both sides.
-x < 6
Multiply both sides by -1.
x > -6
10. Answer :
5 - x > -7
Subtract 5 from both sides.
-x > -12
Multiply both sides by -1.
x < 12
11. Answer :
2 - 3x ≤ 14
Subtract 2 from both sides.
-3x ≤ 12
Divide both sides by -3.
x ≥ -4
12. Answer :
(2x - 3)/4 + 9 ≥ 3 + 4x/3
Least common multiple of the denominators 3 and 4 is 12. Multiply both sides of the equation by 12 to get rid of the denominators.
12[(2x - 3)/4 + 9 ≥ 12[3 + 4x/3]
12(2x - 3)/4 + 12(9) ≥ 12(3) + 12(4x/3)
3(2x - 3) + 108 ≥ 36 + 4(4x)
6x - 9 + 108 ≥ 36 + 16x
6x + 99 ≥ 36 + 16x
Subtract 16x from both sides.
-10x + 99 ≥ 36
Subtract 99 from both sides.
-10x ≥ -63
Divide both sides by 10.
x ≤ 6.3
13. Answer :
A. Write a linear inequality to describe the situation.
Let x represent the number of bunches of broccoli and let y represent the number of packages of carrots.
Write an inequality. Use ≤ for “at most.”
Cost of broccoli plus cost of carrots is at most $7.50
1.25x + 0.75y ≤ $7.50
Solve the inequality for y.
1.25x + 0.75y ≤ 7.50
100(1.25x + 0.75y) ≤ 100(7.50)
125x + 75y ≤ 750
75y ≤ 750 - 125x
75y/75 ≤ 750/75 - 125x/75
y ≤ 10 - (5/3)x
y ≤ -(5/3)x + 10
B. Write a linear inequality to describe the situation.
Step 1 :
Because Lily cannot buy a negative amount of vegetables, the system is graphed only in Quadrant I. Graph the boundary line y = -(5/3)x + 10. Use a solid line for ≤.
Step 2 :
Shade below the line. Lily must buy whole numbers of bunches or packages. All points on or below the line with whole-number coordinates represent combinations of broccoli and carrots that Lily can buy.
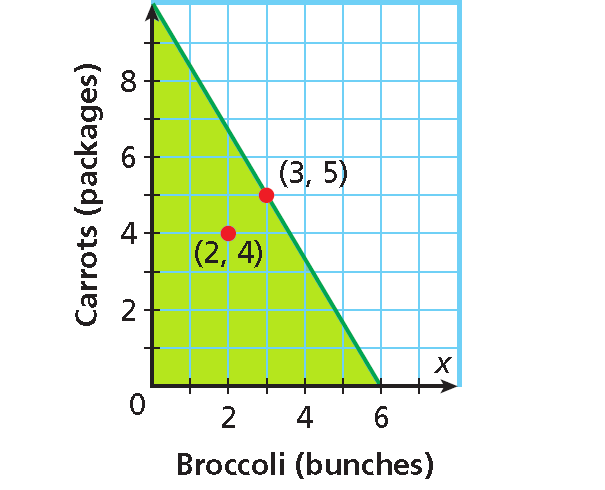
C. Give two combinations of vegetables that Lily can buy.
Two different combinations that Lily could buy for $7.50 or less are 2 bunches of broccoli and 4 packages of carrots, or 3 bunches of broccoli and 5 packages of carrots.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


