INTRODUCTION TO SURFACE AREA AND VOLUME

Surface Area

Surface area refers to the area of the exposed surface of the three dimensional solid.

There are two types of surface area

(i) Lateral surface area 

(ii) Total surface area

• In general, lateral surface area does not include the base of the shape. 
  
• Total surface area is the area of the entire object. Lateral surface area (lateral also means side), does not include the area of the top and bottom.

Volume

The volume of any solid refers to the three dimensional space it occupies, often quantified numerically.One dimensional figures, namely lines and two dimensional shapes, namely squares area assigned zero volume in the  three dimensional space.

Formulas

Cube :

A cube is a right rectangular prism with square upper and lower bases and a square vertical faces.

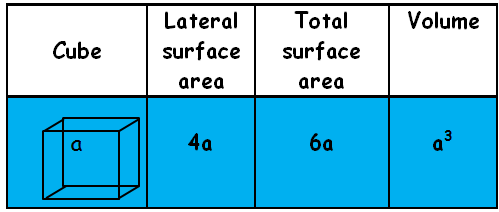
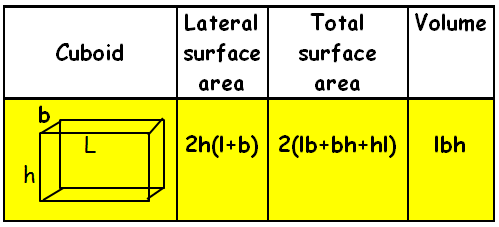
Cuboid :

A cuboid is a three-dimensional shape with a length, width, and a height. The cuboid shape has six sides called faces

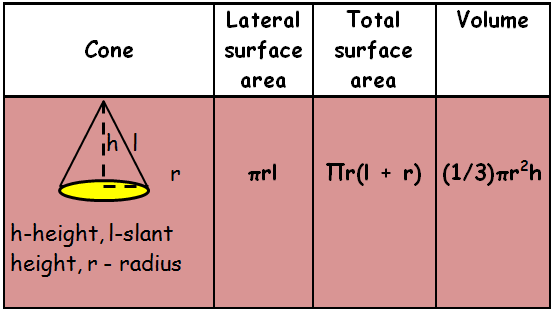
Cone :

A cone is a solid with circular base curved by a curved surface to a single vertex.   Introduction to surface area and volume

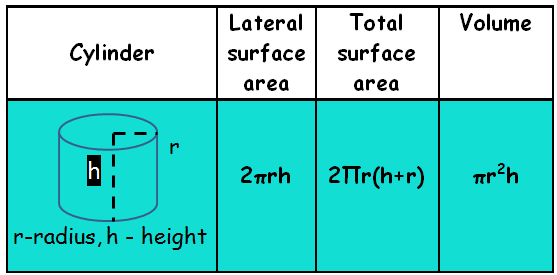
Cylinder :

A Cylinder is a solid with circular base. It can be of the shape of a pillar, a rubber tube, the trunk of a tree, etc. The term circular cylinder is used to describe a right circular cylinder. A circular cylinder  having perpendicular base and height is known as a right circular cylinder. 

Sphere :

A Sphere is a set of points in space that are the same distance from a given point.  Introduction to surface area and volume

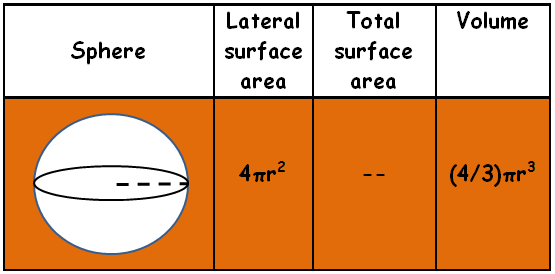
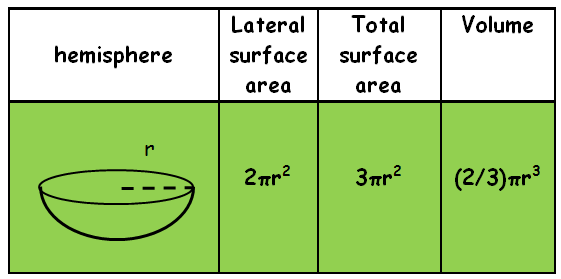
Hemisphere :

A hemisphere is a three-dimensional shape that is half of a sphere with one flat, circular side, which also known as a face.  Introduction to surface area and volume

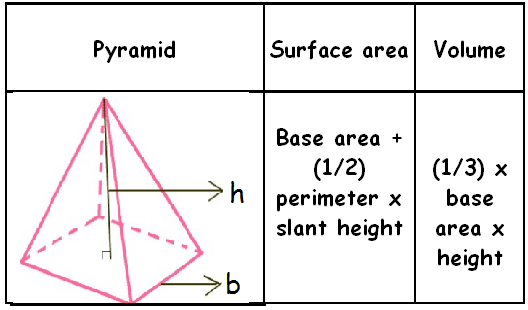
Pyramid :

A pyramid is a polyhedron that has polygon base and three or more triangular faces that meet at a common vertex.

Practical Problems 

Problem 1 :

A wall of length 10 m was to be built across an open ground. The height of the wall is 4 m and thickness of the wall is 24 cm. If this wall is to be built up with bricks whose dimensions are 24 cm × 12 cm × 8 cm, how many bricks would be required ?

Solution :

Since the wall with all its bricks makes up the space occupied by it, we need to find the volume of the wall, which is nothing but a cuboid.

Here, Length = 10 m = 1000 cm

Thickness = 24 cm

Height = 4 m = 400 cm

Volume of the wall = length × thickness × height

=  1000 x 24 x 400 cm

Now, each brick is a cuboid with length = 24 cm, breadth = 12 cm and height = 8 cm

So, volume of each brick = length × breadth × height

=  24 x 12 x 8 cm³

So, number of bricks required =

volume of the wall/volume of each brick

=  (1000 x 24 x 400) / (24 x 12 x 8)

=  4166.6

So, the wall requires 4167 bricks.

Problem 2 :

At a Ramzan Mela, a stall keeper in one of the food stalls has a large cylindrical vessel of base radius 15 cm filled up to a height of 32 cm with orange juice. The juice is filled in small cylindrical glasses of radius 3 cm up to a height of 8 cm. Find the number of glasses that he can fill the juice completely?

Solution :

The volume of juice in the vessel = volume of the cylindrical vessel   =  πr²h

  =  π x 15 x 15 x 32 cm³

Similarly, the volume of juice each glass can hold =  π r²h

(where r and h are taken as the radius and height respectively of each glass)

  =  π x 3 x 3 x 8 cm³

So, number of glasses of juice that are sold

  =  volume of the vessel/volume of each glass 

  =  (π x 15 x 15 x 32) / (π x 3 x 3 x 8)

=  100

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.